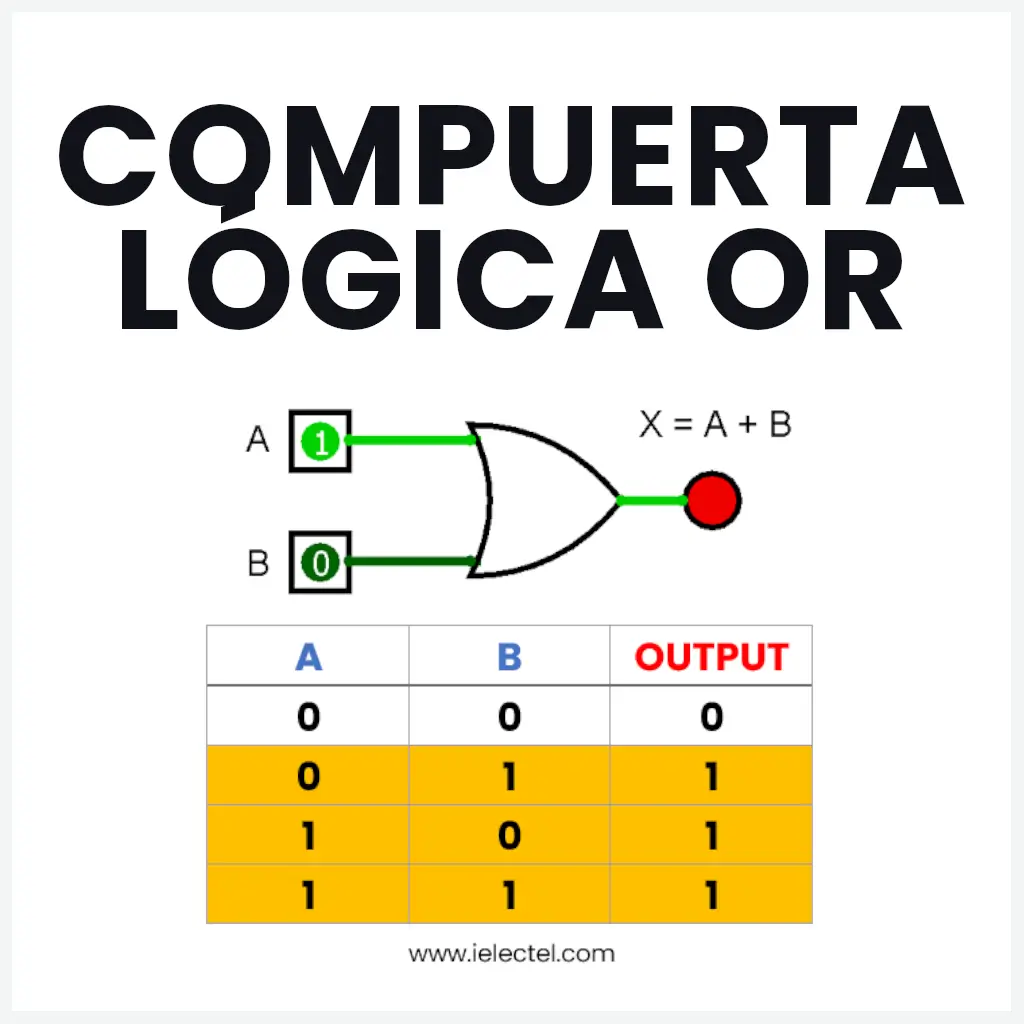
Tablas de Verdad en Electrónica 👨‍💻

Las tablas de verdad son esenciales en el diseño y análisis de circuitos electrónicos, proporcionando una representación sistemática de las relaciones lógicas entre las entradas y salidas. Permiten a los ingenieros electrónicos comprender y anticipar el comportamiento de sus diseños. Este artículo explora los conceptos fundamentales de las tablas de verdad y destaca su papel crucial en la toma de decisiones lógicas en la electrónica.

¿Qué son las Tablas de Verdad?

En su esencia más pura, una tabla de verdad es un mapa que muestra todas las combinaciones posibles de entradas y sus respectivas salidas en un circuito lógico. Las entradas y salidas se representan mediante los valores binarios 0 y 1, o falso y verdadero, proporcionando una visión clara de cómo el circuito responde a diferentes escenarios.

Representación Visual

Para ilustrar este concepto, tomemos una compuerta lógica AND como ejemplo. Esta puerta toma dos entradas (A y B) y produce una salida que es verdadera solo cuando ambas entradas son verdaderas. La tabla de verdad correspondiente se vería así:

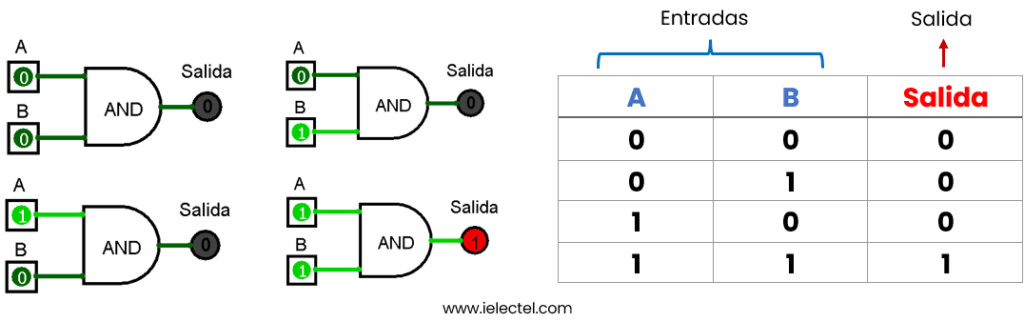
Cada fila de la tabla representa una combinación única de entradas, y la columna de salida muestra el resultado correspondiente.

¿Cómo se lee una tabla de verdad?

Leer una tabla de verdad es esencial para comprender cómo un circuito lógico responde a diferentes combinaciones de entradas. Vamos a desglosar cómo interpretar una tabla de verdad utilizando un ejemplo sencillo. Tomemos la tabla de verdad para una puerta lógica AND:

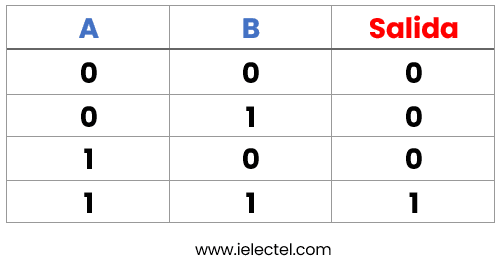
En esta tabla:

• Columna de Entradas (A y B): Representa las diferentes combinaciones posibles de estados para las entradas del circuito. En este caso, A y B pueden ser «0» o «1».
• Columna de Salida: Muestra los resultados correspondientes o el estado de la salida del circuito para cada combinación de entradas.

Ahora, interpretemos cada fila:

1. Primera Fila: A es «0», B es «0». La salida es «0». Esto indica que cuando ambas entradas A y B son «0», la salida del circuito AND es «0».
2. Segunda Fila: A es «0», B es «1». La salida es «0». Indica que cuando A es «0» y B es «1», la salida del circuito AND es «0».
3. Tercera Fila: A es «1», B es «0». La salida es «0». En este caso, cuando A es «1» y B es «0», la salida del circuito AND sigue siendo «0».
4. Cuarta Fila: A es «1», B es «1». La salida es «1». Esto significa que solo cuando ambas entradas A y B son «1», la salida del circuito AND es «1».

En resumen, la tabla de verdad nos proporciona una guía rápida para entender cómo se comporta el circuito lógico en diversas condiciones.

Consejos para Diseñar Tablas de Verdad Eficientes

1. Simplificación Lógica: Reduzca las expresiones lógicas a su forma más simple utilizando leyes algebraicas.
2. Orden Lógico: Organice las combinaciones de entradas en un orden lógico para facilitar la lectura y comprensión.
3. Verificación Cruzada: Asegúrese de que cada combinación de entradas tenga una salida correspondiente y que no falte ninguna.
4. Evitar Redundancias: Elimine filas redundantes para simplificar la tabla sin perder información crucial.

Ejemplo Práctico

Supongamos que tenemos un circuito con tres entradas (A, B y C) y una salida (Z), y queremos que la salida sea «1» solo cuando al menos dos de las tres entradas sean «1». Al analizar las combinaciones posibles, podemos diseñar una expresión lógica y una tabla de verdad para garantizar el comportamiento deseado. Resolvamos este ejemplo siguiendo estos pasos:

Primero: Definir el Problema

• Tenemos un circuito con tres entradas: A, B y C.
• La salida (Z) debe ser «1» solo cuando al menos dos de las tres entradas son «1».

Segundo: Enumerar las Combinaciones Posibles

• Para un sistema de tres entradas, hay 23=823=8 posibles combinaciones.
• Las combinaciones posibles son: 000, 001, 010, 011, 100, 101, 110, 111.

Tercero : Diseñar una Expresión Lógica

• Observamos que la salida debe ser «1» cuando al menos dos de las tres entradas son «1».
• Podemos usar la operación lógica OR para expresar esto.

Cuarto: Expresión Lógica

• La expresión lógica sería: Z =A⋅B+A⋅C+B⋅C
• Esto significa que la salida (Z) será «1» si al menos dos de las tres entradas son «1».

Quinto : Crear la Tabla de Verdad

• Ahora, creamos la tabla de verdad para verificar que la expresión lógica cumple con el comportamiento deseado.

• Analizamos cada fila: La salida (Z) es «1» solo en las filas donde al menos dos de las tres entradas son «1», coincidiendo con nuestro requerimiento.

Sexto: Resultado

• Hemos diseñado una expresión lógica (Z=A⋅B+A⋅C+B⋅C) y una tabla de verdad que garantiza que la salida sea «1» solo cuando al menos dos de las tres entradas son «1». Esto cumple con el comportamiento deseado del circuito.

Conclusión

En conclusión, las tablas de verdad son una herramienta poderosa en el mundo de la electrónica, proporcionando una representación clara y sistemática de las relaciones lógicas en los circuitos. Al comprender su aplicación y seguir buenas prácticas de diseño, los ingenieros pueden crear circuitos más eficientes y tomar decisiones fundamentadas en la lógica. ¡Explora el fascinante mundo de las tablas de verdad y desbloquea el potencial de la electrónica! 👨🏻‍🏫

Preguntas Frecuentes

Invita a otros a explorar: Comparte Ahora 📢