/ Conceptos Fundamentales, Electrónica / Por

¿Qué es el Teorema de Thévenin? Aprende a Simplificar Circuitos Eléctricos

Tabla de contenidos
  1. ¿Qué es el Teorema de Thévenin? Aprende a Simplificar Circuitos Eléctricos

El Teorema de Thévenin es uno de los conceptos más fundamentales en la electrónica y telecomunicaciones. Si alguna vez te has preguntado cómo simplificar un circuito complejo para facilitar su análisis, este teorema es la herramienta que necesitas. En este artículo, te explicaré de manera detallada y clara cómo funciona el teorema de Thévenin y cómo aplicarlo en circuitos eléctricos, de modo que cualquier persona, sin importar su nivel de experiencia, pueda comprenderlo y usarlo.

Breve Historia

El Teorema de Thévenin tiene su origen en el siglo XIX, gracias al ingeniero francés Léon Charles Thévenin. En 1883, mientras trabajaba para la Compañía Francesa de Teléfonos, Thévenin se enfrentó al desafío de analizar y simplificar redes eléctricas complejas, un problema crucial para el diseño y mantenimiento de los sistemas de telecomunicaciones.

Durante este tiempo, los circuitos eléctricos eran difíciles de analizar debido a la cantidad de componentes interconectados. Thévenin se dio cuenta de que podía simplificar cualquier red lineal a un circuito equivalente mucho más sencillo, compuesto solo por una fuente de voltaje y una resistencia en serie. Este descubrimiento facilitó el análisis de circuitos complejos, haciendo que los ingenieros pudieran trabajar con ellos de manera más eficiente y rápida.

Aunque en su momento su trabajo no recibió mucha atención, hoy el Teorema de Thévenin es una herramienta fundamental en la ingeniería eléctrica y las telecomunicaciones. Su legado ha permitido que estudiantes y profesionales alrededor del mundo simplifiquen circuitos de manera práctica y eficaz, ayudando a resolver problemas que antes resultaban abrumadores.

El teorema ha trascendido generaciones y se ha convertido en una de las técnicas más utilizadas en el análisis de circuitos eléctricos, demostrando que incluso una idea sencilla puede revolucionar un campo entero.

¿Qué es el Teorema de Thévenin?

El Teorema de Thévenin establece que cualquier red lineal compuesta por resistencias, fuentes de voltaje y corriente, puede reducirse a un circuito equivalente más sencillo. Este circuito equivalente consta de una sola resistencia en serie con una fuente de voltaje. La idea detrás del teorema es que puedes reemplazar toda la complejidad de un circuito externo por algo mucho más manejable, manteniendo las mismas condiciones en los terminales de salida.

que es el teorema de Thévenin

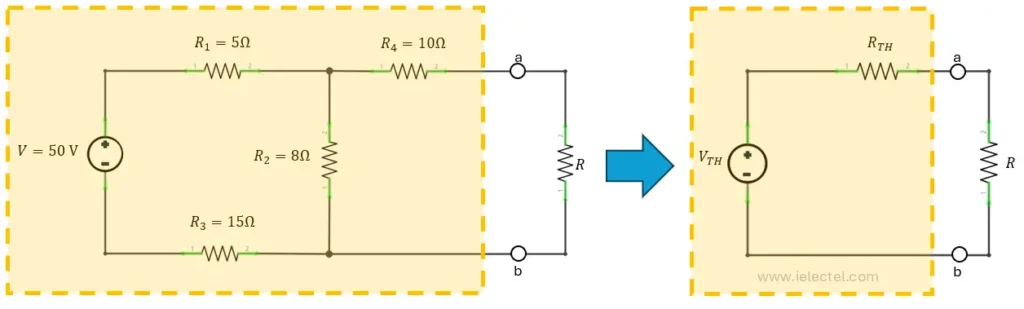
Conceptos Clave:

  • Circuito Lineal: Un circuito que tiene componentes cuya respuesta es directamente proporcional a las señales de entrada.
  • Circuito Equivalente: El circuito reducido que reemplaza al original pero tiene el mismo efecto en la carga conectada.

¿Por qué es importante el Teorema de Thévenin?

Este teorema es una herramienta poderosa porque te permite simplificar el análisis de circuitos complejos. En lugar de lidiar con múltiples componentes, puedes transformarlos en una resistencia y una fuente de voltaje, lo que facilita cálculos como la corriente y la potencia en una carga. Es muy útil para diseñadores de circuitos, ingenieros electrónicos y estudiantes de telecomunicaciones.

Cómo aplicar el Teorema de Thévenin

Paso 1: Identificar el circuito donde aplicar el Teorema de Thévenin

El primer paso para aplicar el Teorema de Thévenin es identificar las terminales donde deseas simplificar el circuito. Imagina que tienes un circuito con varias resistencias y fuentes de voltaje o corriente, y estás interesado en saber qué sucede en una resistencia particular (llamada «carga»).

Como ejemplo práctico usando el teorema de Thevenin, calcularemos la corriente i por el resistor R del siguiente circuito:

¿Qué es el Teorema de Thévenin?

Paso 2: Desconectar la carga del circuito

Para proceder con la aplicación del teorema, debes quitar la resistencia de carga del circuito. Este paso es fundamental, ya que el circuito equivalente de Thévenin se define sin la carga conectada. Esto significa que tendrás un circuito con las mismas resistencias y fuentes, pero sin la resistencia de carga.

Desconectar la Resistencia de Carga R

Primero, identificamos y desconectamos la resistencia R para dejar libres sus terminales. Ahora, tenemos que determinar el circuito equivalente de Thévenin, que consiste en:

  • Una fuente de voltaje de Thévenin V_{th}
  • Una resistencia de Thévenin R_{th}
¿Qué es el Teorema de Thévenin?

Paso 3: Calcular la Resistencia de Thévenin (Rth)

Para encontrar la resistencia de Thévenin entre los terminales, debes seguir los siguientes pasos:

  • Desconecta todas las fuentes de energía en el circuito (esto implica reemplazar las fuentes de voltaje por cortocircuitos y las fuentes de corriente por circuitos abiertos).
  • Luego, calcula la resistencia entre los terminales donde quitaste la carga. La resistencia resultante es tu Rth o resistencia de Thévenin.

Calcular la Resistencia de Thévenin R_{th}

Para encontrar la resistencia de Thévenin R_{th}, eliminamos la fuente de voltaje (reemplazándola por un cortocircuito) y calculamos la resistencia equivalente vista desde los terminales de la resistencia R.

¿Qué es el Teorema de Thévenin?

1. Calcular la Resistencia Equivalente del Paralelo:

Para el paralelo entre la resistencia de 20Ω y la de 4Ω, usamos la fórmula del paralelo:

R_{\text{eq}} = \frac{R_1 \cdot R_2}{R_1 + R_2} = \frac{20\Omega \cdot 4\Omega}{20\Omega + 4\Omega} = \frac{80}{24} = 3.33\Omega

¿Qué es el Teorema de Thévenin?

2. Resistencia Total del Circuito:

La resistencia total del circuito, que es la suma de la resistencia de 5Ω en serie con la resistencia equivalente R_{\text{eq}}​, es:

R_{\text{total}} = 5\Omega + 3.33\Omega = 8.33\Omega

¿Qué es el Teorema de Thévenin?

Por lo tanto, R_{th} = 8\Omega

Paso 4: Calcular el Voltaje de Thévenin V_{th}

El voltaje de Thévenin V_{th} es el voltaje en la resistencia de 5Ω. Sabemos que la resistencia de 5Ω está en paralelo con la de 20Ω, y comparten el mismo voltaje, así que podemos usar el divisor de voltaje para encontrar V_{th}​.

¿Qué es el Teorema de Thévenin?

Calculamos el voltaje en la resistencia de 5Ω usando el divisor de voltaje:

V_{th} = V_{\text{50}} \cdot \frac{R_{\text{2Ω}}}{R_{\text{1Ω}} + R_{\text{2Ω}}} = 50V \cdot \frac{20\Omega}{5\Omega + 20\Omega} = 50V \cdot \frac{20}{25} = 40V

Por lo tanto, V_{th} = 40V.

Paso 5: Reemplazar el circuito original con su equivalente de Thévenin

El siguiente paso es reemplazar todo el circuito por su equivalente de Thévenin, que consiste en:

  • Una fuente de voltaje (Vth) en serie con una resistencia (Rth).
  • Finalmente, reconecta la resistencia de carga al circuito equivalente.
¿Qué es el Teorema de Thévenin?

Este nuevo circuito es mucho más sencillo de analizar. Ahora puedes calcular la corriente que pasa por la carga utilizando la Ley de Ohm:

I = \frac{V_{th}}{R_{th} + R_{L}}

Donde:

  • I es la corriente a través de la carga.
  • R_{th}​ es la resistencia de Thévenin.
  • R_{L} es la resistencia de carga.

Calcular la Corriente i en la Resistencia R

Finalmente, aplicamos la Ley de Ohm para calcular la corriente que pasa por R:

i = \frac{V_{th}}{R_{th} + R} = \frac{40V}{8\Omega + R}

La corriente i depende del valor de R. Si tienes un valor específico para R, puedes sustituirlo en la fórmula para obtener la corriente.

Por ejemplo, si R = 4\Omega:

i = \frac{40V}{8\Omega + 4\Omega} = \frac{40V}{12\Omega} \approx 3.33A

Así que, si R = 4Ω, la corriente sería aproximadamente 3.33A.

Aplicando el Teorema de Thévenin, simplificamos el circuito complejo en un circuito equivalente que consiste en una fuente de voltaje de 40V y una resistencia en serie de 8Ω. Esto nos permite calcular fácilmente la corriente (i) que pasa a través de la resistencia de carga (R).

Conclusión

El Teorema de Thévenin es una herramienta fundamental en el análisis de circuitos eléctricos, ya que permite simplificar circuitos complejos en una configuración mucho más sencilla compuesta por una fuente de voltaje equivalente en serie con una resistencia equivalente. Este teorema facilita el cálculo de corrientes y voltajes en cualquier punto del circuito, particularmente cuando se desea analizar cómo una resistencia de carga interactúa con el resto del sistema.

Su principal ventaja es que, una vez obtenido el circuito equivalente de Thévenin, resulta muy sencillo calcular el comportamiento de diferentes valores de resistencias de carga sin necesidad de rehacer todo el análisis del circuito. Esto es especialmente útil en situaciones prácticas de diseño y análisis de sistemas electrónicos y de telecomunicaciones, donde se deben analizar múltiples escenarios de carga. Además, al reducir la complejidad de los cálculos, ayuda a ahorrar tiempo y a minimizar posibles errores.

En resumen, el Teorema de Thévenin no solo es una poderosa técnica de simplificación matemática, sino también una metodología que incrementa la eficiencia y claridad en el análisis de circuitos eléctricos, siendo indispensable para estudiantes, ingenieros y profesionales en el campo de la electrónica y las telecomunicaciones.

Preguntas Frecuentes

¡Esperamos sinceramente que este post, repleto de contenido valioso, haya sido excepcionalmente útil en tu emocionante travesía hacia el fascinante mundo de la electrónica! 🌟 Te extendemos la invitación a explorar muchos más artículos, proyectos, contenido sobre equipos, software y más en nuestra página web.

Invita a otros a explorar: Comparte Ahora 📢

Entradas Relacionadas

Subscribe
Subscribe
Scroll al inicio