Circuitos en Serie y en Paralelo

Tabla de contenidos

¿Qué es un circuito eléctrico?
¿Qué es un Circuito en Serie?
- Características de un Circuito en Serie:
Resistencias, Capacitores e Inductores en serie
Ventajas y Desventajas de los Circuitos en Serie
¿Qué es un Circuito en Paralelo?
- Características de un Circuito en Paralelo:
Resistencias, Capacitores e Inductores en paralelo
Ventajas y Desventajas de los Circuitos en Paralelo
Comparación entre Circuitos en Serie y Paralelo
¿Cuál es mejor?
Conclusión
Preguntas Frecuentes

Si alguna vez te has preguntado cómo se comportan las luces de navidad cuando una se funde, o por qué tu hogar sigue teniendo electricidad si apagas una lámpara, ¡has llegado al lugar correcto! entender los circuitos en serie y en paralelo es fundamental para cualquier persona que quiera iniciarse en la electrónica. Vamos a explorar ambos tipos de circuitos para que al finalizar esta lectura puedas distinguirlos, comprender sus diferencias y aplicaciones, y hasta experimentar con ellos.

¿Qué es un circuito eléctrico?

Un circuito eléctrico es una conexión cerrada por la que fluye la corriente. Está compuesto de elementos como resistencias, capacitores o inductores, y una fuente de energía, como una batería o una fuente de voltaje. Cuando los componentes se conectan de forma específica, se forman diferentes tipos de circuitos: en serie o en paralelo.

¿Qué es un Circuito en Serie?

Un circuito en serie es un tipo de conexión en el que todos los componentes están dispuestos uno tras otro en la misma trayectoria de corriente. En otras palabras, la corriente eléctrica fluye por un solo camino y pasa por todos los elementos del circuito.

Características de un Circuito en Serie:

Un solo camino para la corriente: La corriente que fluye por el circuito es la misma para todos los componentes.

$I_{\text{total}} = I_1 = I_2 = I_3 = I_4 =.......= I_n$

Compartición de voltaje: La tensión o voltaje de la fuente de energía se divide entre los componentes del circuito. Cuantos más componentes haya, menos voltaje recibirá cada uno.

$V_{\text{total}}=V_1 + V_2 + V_3 + V_4 +.......+ V_n$

Desventaja notable: Si un componente se rompe, daña o se desconecta, se interrumpe el flujo de corriente y todo el circuito deja de funcionar. Es por esto que cuando una bombilla en una cadena de luces de navidad en serie se funde, todas las luces se apagan.

Resistencias, Capacitores e Inductores en serie

Cuando se trata de componentes eléctricos como resistencias, capacitores e inductores, la forma en que están conectados en un circuito afecta su comportamiento global. A continuación, te explicamos en detalle cómo funcionan cuando están en serie.

Resistencias en Serie

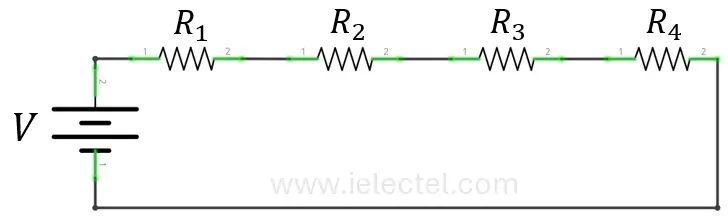
Cuando las resistencias están conectadas en serie, la corriente que pasa por cada una es la misma, pero el voltaje total se distribuye entre ellas. Esto significa que la resistencia total del circuito es la suma de las resistencias individuales.

Fórmulas

Corriente constante: En un circuito en serie, la corriente es la misma a través de todas las resistencias, ya que solo hay un camino para que fluya la corriente.

$I_{\text{total}} = I_{R1} = I_{R2} = I_{R3} = I_{R4} =.......= I_{Rn}$

Voltaje dividido: La tensión total aplicada al circuito se divide entre las resistencias de acuerdo con sus valores. Las resistencias más grandes reciben una mayor parte del voltaje.

$V_{\text{total}}=V_{R1} + V_{R2} + V_{R3} + V_{R4} +.......+ V_{Rn}$

Resistencia total: La resistencia total $R_{\text{total}}$ de un conjunto de resistencias en serie se calcula sumando las resistencias individuales:

$R_{\text{total}} = R_1 + R_2 + R_3 + \dots + R_n$

Ejemplo

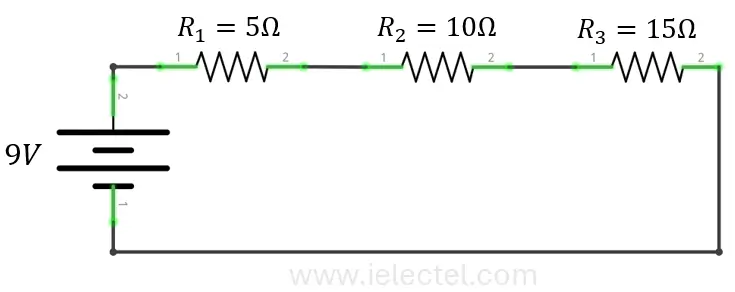
Supongamos que tienes tres resistencias $R_1 = 5\ \Omega$ , $R_2 = 10\ \Omega$ y $R_3 = 15\ \Omega$ conectadas en serie. Queremos calcular la resistencia total del circuito.

Solución:

$R_{\text{total}} = R_1 + R_2 + R_3 = 5\ \Omega + 10\ \Omega + 15\ \Omega = 30\ \Omega$

La resistencia total del circuito es de 30 ohmios.

Aplicamos la Ley de Ohm para determinar la corriente y el voltaje que circula a través de cada resistor:

$I_{total} = \frac{V}{R_{\text{total}}} = \frac{9V}{30\ \Omega} = 0.3\ A$

La corriente que circula por cada resistor es de 0.3 Amperios.

Para calcular el voltaje total del circuito, es necesario determinar el voltaje que cae en cada resistor individualmente, sumando estas caídas para obtener el valor total.

$V_{R1} = 0.3 \, A \cdot 5 \, \Omega = 1.5 \, V$

$V_{R2} = 0.3 \, A \cdot 10 \, \Omega = 3 \, V$

$V_{R3} = 0.3 \, A \cdot 15 \, \Omega = 4.5\, V$

El voltaje total del circuito está dado por:

$V_{\text{total}}=V_{R1} + V_{R2} + V_{R3}$

$V_{\text{total}}=1.5 V + 3 V + 4.5V = 9V$

Simulación

Vamos a compartir un circuito en Tinkercad para que puedas observar de manera interactiva cómo funcionan las resistencias en serie. Con esta herramienta podrás simular el comportamiento del circuito y visualizar cómo la corriente fluye a través de cada resistencia, además de comprobar cómo se distribuye el voltaje total entre ellas. Esta es una excelente forma de experimentar con circuitos sin necesidad de componentes físicos, facilitando tu comprensión de los conceptos teóricos en la práctica.

Aplicaciones

Los circuitos en serie se usan donde es importante que la misma corriente pase por todos los componentes, como en los circuitos de iluminación antiguos o en algunas aplicaciones de seguridad.

Capacitores en Serie

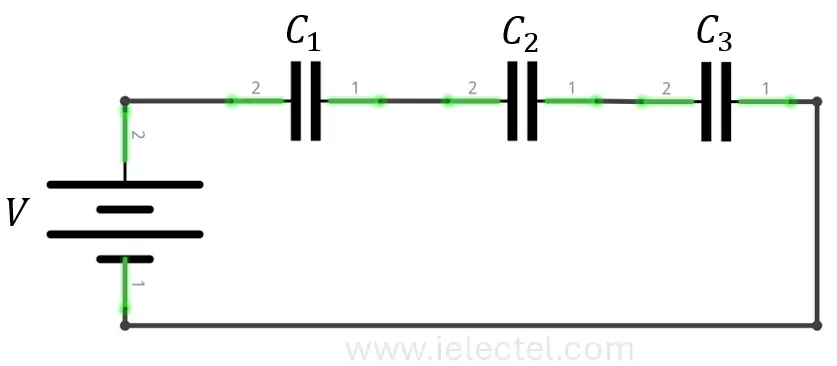
En una configuración de capacitores en serie, la carga en cada capacitor es la misma, pero el voltaje total se reparte entre ellos. La capacidad total en serie es siempre menor que la capacidad de cualquiera de los capacitores individuales.

Fórmulas

Carga constante: La cantidad de carga almacenada en cada capacitor es la misma en un circuito en serie.

Corriente constante: En un circuito en serie, la corriente es la misma a través de todas las resistencias, ya que solo hay un camino para que fluya la corriente.

$I_{\text{total}} = I_{C1} = I_{C2} = I_{C3} = I_{C4} =.......= I_{Cn}$

Voltaje dividido: El voltaje total se reparte entre los capacitores de acuerdo con sus capacidades. Los capacitores más pequeños reciben un mayor voltaje.

$V_{\text{total}}=V_{C1} + V_{C2} + V_{C3} + V_{C4} +.......+ V_{Cn}$

Capacitancia total: La capacitancia total de capacitores en serie es menor que la de cualquier capacitor individual. Se calcula con la fórmula:

$\frac{1}{C_{total}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \dots + \frac{1}{C_n}$

Ejemplo

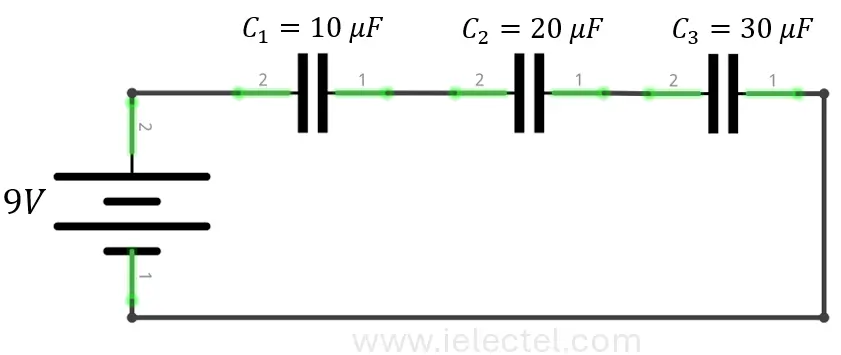
Consideremos tres capacitores $C_1 = 10\ \mu F$ , $C_2 = 20\ \mu F$ y $C_3 = 30\ \mu F$ conectados en serie. Queremos encontrar la capacitancia total.

Solución:

$\frac{1}{C_{\text{total}}} = \frac{1}{10} + \frac{1}{20} + \frac{1}{30}$

Calculamos los términos individualmente:

$\frac{1}{10} = 0.1, \quad \frac{1}{20} = 0.05, \quad \frac{1}{30} \approx 0.0333$

Sumamos las fracciones:

$\frac{1}{C_{\text{total}}} = 0.1 + 0.05 + 0.0333 = 0.1833$

Ahora invertimos el valor para obtener $C_{\text{total}}$ :

$C_{\text{total}} = \frac{1}{0.1833} \approx 5.45\ \mu F$

La capacitancia total del circuito es de aproximadamente 5.45 microfaradios.

Para calcular el voltaje total del circuito, es necesario determinar el voltaje que cae en cada resistor individualmente, sumando estas caídas para obtener el valor total. Para llegar a este punto primero debemos de calcular la carga total del circuito, en un circuito en serie la carga total es la misma para todos los capacitores y se calcula como:

$Q_{{\text{total}}} = C_{\text{total}} \cdot V_{\text{fuente}}$

$Q_{{\text{total}}} = 5.45\ \mu F \cdot 9V \approx 49.05\ \mu C$

El voltaje en cada capacitor se calcula como:

$V_{C1}=\frac{Q_{{\text{total}}}}{C_1}=\frac{49.05\ \mu C}{10\ \mu F}\approx 4.91 V$

$V_{C1}==\frac{49.05\ \mu C}{20\ \mu F}\approx 2.45 V$

$V_{C1}=\frac{49.05\ \mu C}{30\ \mu F}\approx 1.64 V$

La suma de los voltajes en cada capacitor debe ser igual al voltaje total aplicado:

$V_{\text{total}}=4.91 V + 2.45 V + 1.64 V = 9V$

Simulación

Vamos a compartir un circuito en Tinkercad para que puedas observar de manera interactiva cómo funcionan los capacitores en serie. Con esta herramienta podrás simular el comportamiento del circuito y visualizar cómo la corriente fluye a través de cada capacitor, además de comprobar cómo se distribuye el voltaje total entre ellas. Esta es una excelente forma de experimentar con circuitos sin necesidad de componentes físicos, facilitando tu comprensión de los conceptos teóricos en la práctica.

Aplicaciones

Los capacitores en serie se usan en circuitos de alta tensión, ya que dividen la tensión entre los capacitores, lo que reduce la tensión en cada uno de ellos.

Inductores en Serie

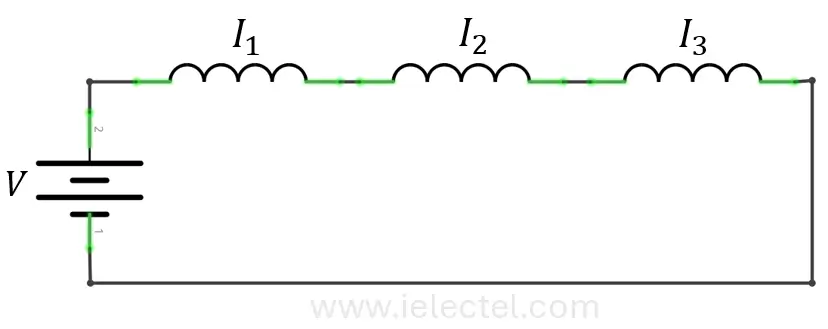
Cuando los inductores están conectados en serie, la inductancia total del circuito es la suma de las inductancias individuales. Esto se debe a que el campo magnético se combina y no se cancela, al igual que ocurre con las resistencias.

Fórmulas

Corriente constante: La corriente que pasa a través de cada inductor es la misma.

$I_{\text{total}} = I_{I1} = I_{I2} = I_{I3} = I_{I4} =.......= I_{In}$

Voltaje dividido: El voltaje total aplicado al circuito se distribuye entre los inductores.

$V_{\text{total}}=V_{I1} + V_{I2} + V_{I3} + V_{I4} +.......+ V_{In}$

Inductancia total: La inductancia total de inductores en serie es la suma de las inductancias individuales:

$L_{total} = L_1 + L_2 + L_3 + \dots + L_n$

Ejemplo

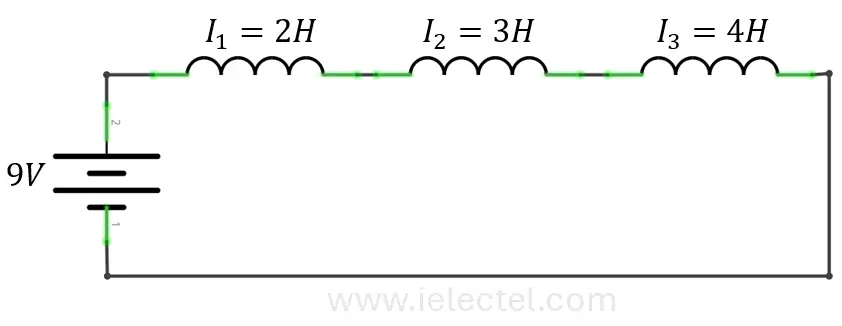
Supongamos que tienes tres inductores $L_1 = 2\ H$ , $L_2 = 3\ H$ , y $L_3 = 4\ H$ conectados en serie. Queremos calcular la inductancia total.

Solución:

$L_{\text{total}} = L_1 + L_2 + L_3 = 2\ H + 3\ H + 4\ H = 9\ H$

La inductancia total es de 9 henrios.

Como los inductores están en serie, la corriente que pasa por cada inductor es la misma y es determinada por la Ley de Ohm generalizada para un circuito RL (Resistencia-Inductancia). La corriente en un circuito con inductancia en corriente continua está dada por:

$I = \frac{V}{L_{\text{total}}}$

$I = \frac{9V}{9H}=1A$

Para calcular el voltaje a través de cada inductor ( $V_L$ ), podemos usar la Ley de Faraday para los inductores, que establece que el voltaje en un inductor es proporcional a la inductancia y a la tasa de cambio de corriente, dada por:

$V_L = L \cdot \frac{dI}{dt}$

Dado que en corriente continua (DC) después de un tiempo prolongado ( $t \to \infty$ ) la tasa de cambio de la corriente ( $\frac{dI}{dt}$ ) es cero, no hay variación de corriente en el tiempo y por lo tanto, en estado estacionario no hay caída de voltaje en los inductores en DC.

Sin embargo, si hablamos de voltaje bajo condiciones transitorias o cuando el circuito se energiza por primera vez, el voltaje en cada inductor se puede calcular simplemente como:

$V_L = L \cdot I$

Para cada inductor, calculamos el voltaje usando la corriente obtenida ( $I = 1A$ ):

$V_{L_1} = 2H \cdot 1A = 2V$

$V_{L_2} = 3H \cdot 1A = 3V$

$V_{L_3} = 4H \cdot 1A = 4V$

La suma de los voltajes en los inductores debe ser igual al voltaje total de la fuente:

$V_{\text{total}} = V_{L_1} + V_{L_2} + V_{L_3} = 2V + 3V + 4V = 9V$

Simulación

Vamos a compartir un circuito en Tinkercad para que puedas observar de manera interactiva cómo funcionan los inductores en serie. Con esta herramienta podrás simular el comportamiento del circuito y visualizar cómo la corriente fluye a través de cada inductor, además de comprobar cómo se distribuye el voltaje total entre ellas. Esta es una excelente forma de experimentar con circuitos sin necesidad de componentes físicos, facilitando tu comprensión de los conceptos teóricos en la práctica.

Aplicaciones

Los inductores en serie se usan en aplicaciones donde se necesita una mayor inductancia, como en filtros de señales de audio o radiofrecuencia.

Ventajas y Desventajas de los Circuitos en Serie

Ventajas de los Circuitos en Serie

Simplicidad en el diseño:
Los circuitos en serie son más fáciles de diseñar e implementar, especialmente cuando se busca una configuración simple en la que todos los componentes estén conectados uno tras otro. No requieren un cableado complejo, lo que simplifica la construcción del circuito.
Menor cantidad de cableado:
Dado que todos los componentes están conectados en una sola ruta de corriente, se necesita menos cableado en comparación con otros tipos de configuraciones, lo que reduce el costo de materiales y la complejidad del diseño.
Compatibilidad con dispositivos de protección:
Un fusible o interruptor colocado en cualquier parte de un circuito en serie protegerá todo el circuito, ya que la corriente que fluye es la misma para todos los componentes. Esto es útil en situaciones donde se necesita controlar o monitorear el estado del circuito con un solo punto de intervención.
Simplicidad en el cálculo de corriente:
En un circuito en serie, la corriente que fluye es la misma para todos los componentes. Esto facilita los cálculos de corriente y permite diseñar sistemas sencillos donde el control de corriente es esencial, como en algunos sistemas de iluminación.

Desventajas de los Circuitos en Serie

Fallo de un componente afecta a todo el circuito:
Esta es una de las mayores desventajas. Si cualquier componente en un circuito en serie falla (por ejemplo, una bombilla se quema o un interruptor se abre), todo el circuito se interrumpe y los demás componentes dejan de funcionar. Este tipo de configuración no es adecuado para aplicaciones donde la continuidad del servicio es crucial.
Distribución del voltaje:
En un circuito en serie, el voltaje total de la fuente se divide entre los componentes, lo que significa que cada uno recibe solo una fracción del voltaje total. Si se conecta un número elevado de componentes, cada uno recibirá un voltaje reducido, lo que puede ser inadecuado para algunos dispositivos que requieren un voltaje constante para funcionar correctamente.
Dificultad para controlar la potencia individual de los componentes:
Dado que la corriente es la misma para todos los componentes, puede ser difícil controlar individualmente cuánta potencia se entrega a cada componente sin afectar a los demás. Esto limita la flexibilidad del circuito para aplicaciones más avanzadas.
Resistencia acumulativa:
Al conectar múltiples resistencias en serie, la resistencia total aumenta, lo que puede reducir la corriente total del circuito. Esto puede ser un problema en aplicaciones donde se necesita una corriente elevada.

¿Qué es un Circuito en Paralelo?

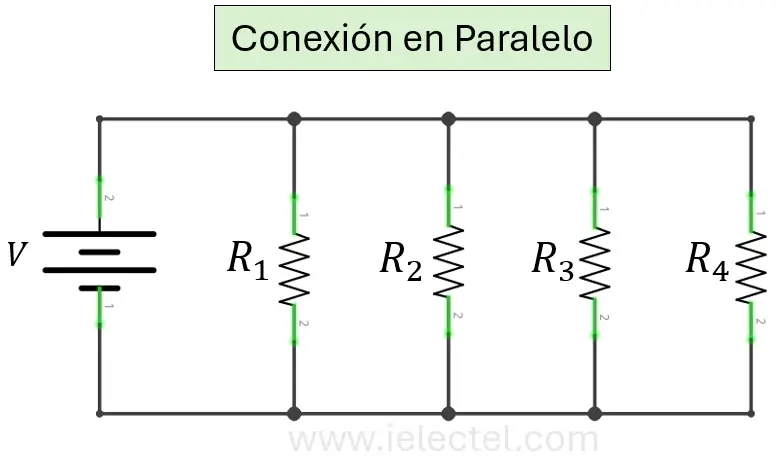
Un circuito en paralelo es aquel en el que los componentes están conectados en múltiples trayectorias, de manera que la corriente puede fluir por más de un camino.

Características de un Circuito en Paralelo:

Varios caminos para la corriente: La corriente eléctrica se divide entre los diferentes caminos, pero el voltaje en cada rama es el mismo.

$I_{\text{total}} = I_1 + I_2 + I_3 + I_4 +.......+ I_n$

Voltaje constante: Todos los componentes conectados en paralelo reciben el mismo voltaje.

$V_{\text{total}} = V_1 = V_2 = V_3 = V_4 =.......= V_n$

Ventaja significativa: Si uno de los componentes falla, los otros siguen funcionando, ya que la corriente aún puede fluir por las otras ramas.

Resistencias, Capacitores e Inductores en paralelo

Cuando se trata de componentes eléctricos como resistencias, capacitores e inductores, la forma en que están conectados en un circuito afecta su comportamiento global. A continuación, se explica en detalle cómo funcionan cuando están en paralelo.

Resistencias en Paralelo

En una conexión de resistencias en paralelo, cada resistencia tiene el mismo voltaje aplicado, pero la corriente se divide entre ellas. La resistencia total en paralelo siempre es menor que la resistencia más pequeña del conjunto.

Fórmulas

Voltaje constante: El voltaje aplicado a cada resistencia es el mismo, ya que están conectadas a los mismos puntos.

$V_{\text{total}} = V_{R1} = V_{R2} = V_{R3} = V_{R4} =.......= V_{Rn}$

Corriente dividida: La corriente se divide entre las resistencias de acuerdo con sus valores. Las resistencias más pequeñas permiten que pase más corriente.

$I_{\text{total}} = I_{R1} + I_{R2} + I_{R3} + I_{R4} +.......+ I_{Rn}$

Resistencia total: La resistencia total es menor que la resistencia más baja y se calcula con la fórmula:

$\frac{1}{R_{total}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$

Ejemplo

Consideremos tres resistencias $R_1 = 4\ \Omega$ , $R_2 = 6\ \Omega$ , y $R_3 = 12\ \Omega$ conectadas en paralelo. Queremos encontrar la resistencia total.

Solución:

$\frac{1}{R_{\text{total}}} = \frac{1}{4} + \frac{1}{6} + \frac{1}{12}$

Calculamos los términos individuales:

$\frac{1}{4} = 0.25, \quad \frac{1}{6} \approx 0.1667, \quad \frac{1}{12} \approx 0.0833$

Sumamos las fracciones:

$\frac{1}{R_{\text{total}}} = 0.25 + 0.1667 + 0.0833 = 0.5$

Invertimos el resultado para obtener $R_{\text{total}}$ :

$R_{\text{total}} = \frac{1}{0.5} = 2\ \Omega$

La resistencia total es de 2 ohmios.

Aplicamos la Ley de Ohm para determinar la corriente y el voltaje que circula a través de cada resistor:

$I_{R1} = \frac{V}{R_{R1} }= \frac{9V}{4\ \Omega} = 2.25\ A$

$I_{R2} = \frac{V}{R_{R2} }= \frac{9V}{6\ \Omega} = 1.5\ A$

$I_{R3} = \frac{V}{R_{R3}} = \frac{9V}{12\ \Omega} = 0.75\ A$

La corriente total del circuito está dado por:

$I_{\text{total}}=I_{R1} + I_{R2} + I_{R3}$

$I_{\text{total}}= 2.25A+ 1.5A + 0.75A = 4.5A$

La corriente que circula por cada resistor es de 4.5 Amperios.

Para calcular el voltaje total del circuito multiplicamos $I_{\text{total}} \cdot R_{\text{total}}$ :

$V_{\text{total}} = I_{\text{total}} \cdot R_{\text{total}}$

$V_{\text{total}}= 4.5 \, A \cdot 2 \, \Omega = 9 \, V$

$V_{\text{total}} = V_1 = V_2 = V_3 = V_4 =.......= V_n$

Simulación

Vamos a compartir un circuito en Tinkercad para que puedas observar de manera interactiva cómo funcionan las resistencias en paralelo. Con esta herramienta podrás simular el comportamiento del circuito y visualizar cómo la corriente fluye a través de cada resistencia, además de comprobar cómo se distribuye el voltaje total entre ellas. Esta es una excelente forma de experimentar con circuitos sin necesidad de componentes físicos, facilitando tu comprensión de los conceptos teóricos en la práctica.

Aplicaciones

Los circuitos de resistencias en paralelo se usan donde se necesita que los componentes funcionen independientemente unos de otros, como en los sistemas eléctricos de hogares.

Capacitores en Paralelo

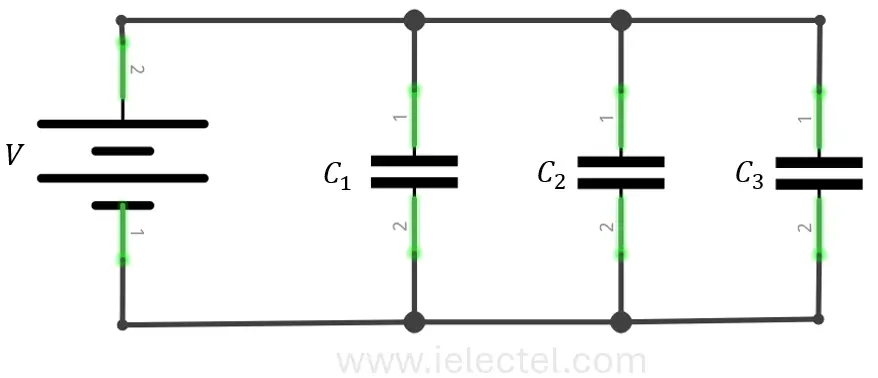
Cuando los capacitores están conectados en paralelo, la capacitancia total es la suma de las capacitancias individuales, ya que la superficie efectiva del capacitor se incrementa.

Fórmulas

Voltaje constante: Todos los capacitores tienen el mismo voltaje en sus terminales.

$V_{\text{total}} = V_{C1} = V_{C2} = V_{C3} = V_{C4} =.......= V_{Cn}$

Carga dividida: La carga se reparte entre los capacitores, pero la suma de las cargas es mayor.

$I_{\text{total}} = I_{C1} + I_{C2} + I_{C3} + I_{C4} +.......+ I_{Cn}$

Capacitancia total: La capacitancia total es la suma de las capacitancias individuales:

$C_{total} = C_1 + C_2 + C_3 + \dots + C_n$

Ejemplo

Consideremos tres capacitores $C_1 = 5\ \mu F$ , $C_2 = 10\ \mu F$ y $C_3 = 15\ \mu F$ conectados en paralelo. Queremos encontrar la capacitancia total.

Solución:

$C_{\text{total}} = C_1 + C_2 + C_3 = 5\ \mu F + 10\ \mu F + 15\ \mu F = 30\ \mu F$

La capacitancia total del circuito es de 30 microfaradios.

Simulación

Vamos a compartir un circuito en Tinkercad para que puedas observar de manera interactiva cómo funcionan los capacitores en paralelo. Con esta herramienta podrás simular el comportamiento del circuito y visualizar cómo la corriente fluye a través de cada capacitor, además de comprobar cómo se distribuye el voltaje total entre ellas. Esta es una excelente forma de experimentar con circuitos sin necesidad de componentes físicos, facilitando tu comprensión de los conceptos teóricos en la práctica.

Aplicaciones

Los capacitores en paralelo se usan en sistemas donde se requiere mayor capacitancia, como en filtros de potencia o en circuitos de almacenamiento de energía.

Inductores en Paralelo

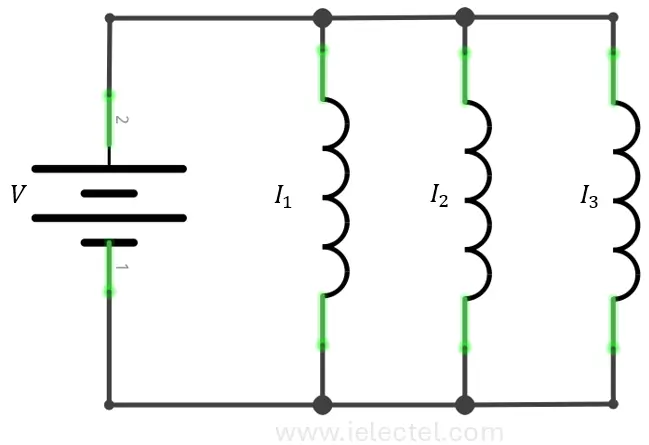
En una conexión de inductores en paralelo, la inductancia total es siempre menor que la inductancia más pequeña. Al igual que con resistencias en paralelo, la corriente se divide entre las ramas.

Fórmulas

Voltaje constante: Todos los inductores en paralelo tienen el mismo voltaje aplicado.

$V_{\text{total}} = V_{I1} = V_{I2} = V_{I3} = V_{I4} =.......= V_{In}$

Corriente dividida: La corriente total se distribuye entre los inductores según su inductancia.

$I_{\text{total}} = I_{I1} = I_{I2} = I_{I3} = I_{I4} =.......= I_{In}$

Inductancia total: La inductancia total de inductores en paralelo es menor que la inductancia más baja, y se calcula con la fórmula:

$\frac{1}{L_{total}} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} + \dots + \frac{1}{L_n}$

Ejemplo

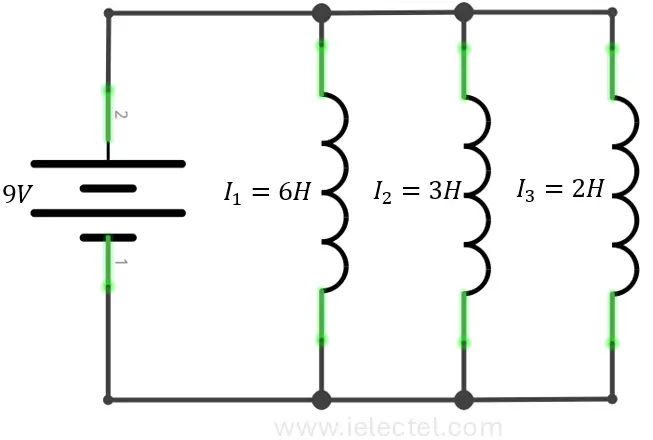
Supongamos que tienes tres inductores $L_1 = 6\ H$ , $L_2 = 3\ H$ , y $L_3 = 2\ H$ conectados en paralelo. Queremos encontrar la inductancia total.

Solución:

$\frac{1}{L_{\text{total}}} = \frac{1}{6} + \frac{1}{3} + \frac{1}{2}$

Calculamos los términos individuales:

$\frac{1}{6} \approx 0.1667, \quad \frac{1}{3} \approx 0.3333, \quad \frac{1}{2} = 0.561$

Sumamos las fracciones:

$\frac{1}{L_{\text{total}}} = 0.1667 + 0.3333 + 0.5 = 1.0$

Invertimos el resultado para obtener $L_{\text{total}}$ :

$L_{\text{total}} = \frac{1}{1.0} = 1\ H$

La inductancia total es de 1 Henrio.

Simulación

Vamos a compartir un circuito en Tinkercad para que puedas observar de manera interactiva cómo funcionan los inductores en paralelo. Con esta herramienta podrás simular el comportamiento del circuito y visualizar cómo la corriente fluye a través de cada inductor, además de comprobar cómo se distribuye el voltaje total entre ellas. Esta es una excelente forma de experimentar con circuitos sin necesidad de componentes físicos, facilitando tu comprensión de los conceptos teóricos en la práctica.

Aplicaciones

Los inductores en paralelo se usan en circuitos donde se requiere una menor inductancia, como en sistemas de distribución de potencia o en aplicaciones de eliminación de ruido.

Ventajas y Desventajas de los Circuitos en Paralelo

Ventajas de los Circuitos en Paralelo

Independencia de los componentes:
Una de las principales ventajas de los circuitos en paralelo es que si un componente falla o se desconecta, los demás siguen funcionando sin problemas. Esto es crucial en aplicaciones como las redes eléctricas domésticas, donde es necesario que los dispositivos funcionen de manera independiente.
Voltaje constante para todos los componentes:
En un circuito en paralelo, todos los componentes reciben el mismo voltaje que el de la fuente. Esto es beneficioso en situaciones donde varios dispositivos necesitan funcionar a un voltaje específico, como en los hogares, donde todos los electrodomésticos deben recibir el mismo suministro de voltaje (por ejemplo, 110V o 220V).
Facilidad para agregar componentes:
En un circuito en paralelo, es sencillo agregar nuevos componentes sin afectar significativamente el rendimiento de los otros dispositivos ya conectados. Cada componente tiene su propia trayectoria de corriente, lo que lo hace ideal para sistemas en expansión, como las instalaciones eléctricas.
Reducción de la resistencia total:
En un circuito en paralelo, la resistencia total del circuito es menor que la resistencia del componente más pequeño. Esto permite que circule más corriente por el circuito en comparación con una configuración en serie con los mismos componentes.
Optimización de la potencia individual:
Dado que los componentes en paralelo tienen el mismo voltaje, es posible controlar la cantidad de corriente que pasa por cada uno sin afectar a los demás, lo que permite un mejor control sobre la potencia de cada dispositivo conectado.

Desventajas de los Circuitos en Paralelo

Mayor complejidad en el diseño:
Los circuitos en paralelo requieren más cableado, lo que aumenta la complejidad del diseño y la cantidad de materiales necesarios. Esto puede hacer que sean más costosos y más difíciles de implementar que los circuitos en serie.
Mayor consumo de energía:
Los circuitos en paralelo tienden a consumir más corriente debido a que la resistencia total disminuye cuando se agregan más ramas. Si no se gestiona adecuadamente, este mayor consumo puede sobrecargar la fuente de energía.
Fusibles o dispositivos de protección por rama:
A diferencia de un circuito en serie, donde un solo fusible puede proteger todo el sistema, en un circuito en paralelo cada rama puede necesitar su propio fusible o interruptor para asegurar que, en caso de fallo en una rama, las otras no se vean afectadas.
Corriente total alta:
A medida que se agregan más ramas con resistencias en paralelo, la corriente total que demanda el circuito aumenta. Esto puede exigir fuentes de alimentación de mayor capacidad, lo que eleva los costos y las demandas del sistema.
Dificultad en el cálculo de la resistencia total:
Aunque las fórmulas para el cálculo de resistencias en paralelo son conocidas, el proceso es más complicado que en los circuitos en serie. Especialmente cuando hay más de dos o tres resistencias, el cálculo de la resistencia total requiere más pasos y puede volverse más tedioso.

Comparación entre Circuitos en Serie y Paralelo

Aquí tienes una tabla comparativa entre circuitos en serie y circuitos en paralelo, resaltando sus principales características:

\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}

Característica	Circuitos en Serie	Circuitos en Paralelo
Conexión de componentes	Los componentes están conectados uno tras otro.	Los componentes están conectados en ramas separadas.
Corriente	La corriente es la misma a través de todos los componentes.	La corriente se divide entre las ramas, dependiendo de la resistencia de cada una.
Voltaje	El voltaje total es la suma de los voltajes en cada componente.	El voltaje es el mismo en todos los componentes.
Resistencia Total	La resistencia total es la suma de todas las resistencias individuales: $R_t = R_1 + R_2 + \dots + R_n$ .	La resistencia total es menor que la resistencia más pequeña: $\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}$ .
Falla de un componente	Si un componente falla, todo el circuito deja de funcionar.	Si un componente falla, los demás siguen funcionando, ya que las otras ramas siguen conectadas.
Aplicaciones comunes	Iluminación en serie de luces navideñas, circuitos de control.	Circuitos domésticos, iluminación de edificios.
Uso de energía	Mayor pérdida de energía debido a la suma de las resistencias.	Menor pérdida de energía porque la corriente se distribuye entre las ramas.
Complejidad del diseño	Diseño sencillo, pero menos eficiente en términos de distribución de energía.	Diseño más complejo, pero más eficiente y flexible.
Efecto de la adición de resistencias	Al agregar más resistencias, la resistencia total aumenta y la corriente disminuye.	Al agregar más resistencias, la resistencia total disminuye y la corriente aumenta en las ramas.

¿Cuál es mejor?

No se trata de que uno sea «mejor» que el otro, sino que cada tipo de circuito tiene ventajas y desventajas según el contexto en que se use. Los circuitos en serie son más fáciles de construir, pero no son tan confiables si uno de los componentes falla. Los circuitos en paralelo son más complejos, pero proporcionan mayor seguridad y flexibilidad en el sistema.

Conclusión

Tanto los circuitos en serie como en paralelo son esenciales para entender el flujo de corriente eléctrica. Los circuitos en serie permiten que la corriente fluya por todos los componentes uno tras otro, mientras que los circuitos en paralelo dividen el flujo de corriente para que cada componente funcione de manera independiente. Al comprender estas dos configuraciones, podrás analizar y diseñar circuitos más complejos en el futuro. ¡Sigue explorando el fascinante mundo de la electrónica!

Preguntas Frecuentes

¿Por qué la resistencia total es menor en un circuito en paralelo?

En un circuito en paralelo, la corriente se divide entre las ramas, lo que hace que la resistencia total sea menor que la resistencia más baja del circuito.

¿Qué tipo de circuito se usa en los hogares?

Los circuitos en paralelo son los más comunes en las casas, ya que permiten que los electrodomésticos funcionen de manera independiente.

¿Cómo se calcula la resistencia total en un circuito en serie?

La resistencia total en un circuito en serie es simplemente la suma de las resistencias individuales.

¿Cuál es más seguro, un circuito en serie o en paralelo?

Los circuitos en paralelo son generalmente más seguros, ya que el fallo de un componente no afecta al resto del sistema.

¿Qué pasa si un componente falla en un circuito en serie?

Si un componente falla en un circuito en serie, el flujo de corriente se interrumpe y todos los demás componentes dejarán de funcionar.

¡Esperamos sinceramente que este post, repleto de contenido valioso, haya sido excepcionalmente útil en tu emocionante travesía hacia el fascinante mundo de la electrónica! 🌟 Te extendemos la invitación a explorar muchos más artículo s, proyectos, contenido sobre equipos, software y más en nuestra página web.

Invita a otros a explorar: Comparte Ahora 📢

Circuitos en Serie y en Paralelo

¿Qué es un circuito eléctrico?

¿Qué es un Circuito en Serie?

Características de un Circuito en Serie:

Resistencias, Capacitores e Inductores en serie

Resistencias en Serie

Fórmulas

Ejemplo

Simulación

Aplicaciones

Capacitores en Serie

Fórmulas

Ejemplo

Simulación

Aplicaciones

Inductores en Serie

Fórmulas

Ejemplo

Simulación

Aplicaciones

Ventajas y Desventajas de los Circuitos en Serie

Ventajas de los Circuitos en Serie

Desventajas de los Circuitos en Serie

¿Qué es un Circuito en Paralelo?

Características de un Circuito en Paralelo:

Resistencias, Capacitores e Inductores en paralelo

Resistencias en Paralelo

Fórmulas

Ejemplo

Simulación

Aplicaciones

Capacitores en Paralelo

Fórmulas

Ejemplo

Simulación

Aplicaciones

Inductores en Paralelo

Fórmulas

Ejemplo

Simulación

Aplicaciones

Ventajas y Desventajas de los Circuitos en Paralelo

Ventajas de los Circuitos en Paralelo

Desventajas de los Circuitos en Paralelo

Comparación entre Circuitos en Serie y Paralelo

¿Cuál es mejor?

Conclusión

Preguntas Frecuentes

Entradas Relacionadas