Descripción Algebraica de Circuitos Lógicos 🅰️➕🅱️
La descripción algebraica de circuitos lógicos es una herramienta fundamental en el diseño y análisis de sistemas digitales. En este artículo, exploraremos qué significa exactamente esta disciplina y cómo se aplican conceptos algebraicos para comprender y representar circuitos lógicos.
¿Qué es una descripción algebraica?
Una descripción algebraica es una representación matemática y simbólica que utiliza símbolos y operaciones algebraicas para expresar de manera formal las relaciones y propiedades de un conjunto o sistema. En el contexto de circuitos lógicos y sistemas digitales, la descripción algebraica se refiere a la representación de las funciones lógicas utilizando álgebra booleana.
La utilidad de la descripción algebraica en electrónica y sistemas digitales radica en que proporciona una forma concisa y matemática de expresar el comportamiento de los circuitos lógicos. Facilita el diseño, análisis y optimización de sistemas digitales al permitir representar funciones complejas mediante expresiones algebraicas que pueden simplificarse y entenderse de manera más eficiente.
¿Qué elementos intervienen en la descripción algebraica ?
En el corazón de cualquier circuito lógico se encuentran las compuertas lógicas. Estas son dispositivos electrónicos que realizan operaciones lógicas básicas y son los bloques de construcción esenciales de los sistemas digitales. Las compuertas más comunes son las compuertas AND, OR y NOT.
- Compuerta AND: Representada por un símbolo de multiplicación (*) en la descripción algebraica, la compuerta AND devuelve un valor lógico verdadero (1) solo si todas sus entradas son verdaderas. Ejemplo: Si A y B son dos entradas, la expresión algebraica sería A * B.
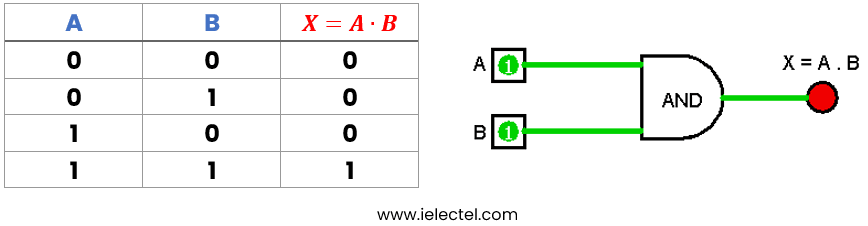
- Compuerta OR: Representada por un símbolo de suma (+), la compuerta OR devuelve un valor lógico verdadero si al menos una de sus entradas es verdadera. Ejemplo: Para dos entradas, la expresión algebraica sería A + B.

- Compuerta NOT: Representada por una barra sobre la variable, la compuerta NOT invierte el valor lógico de su entrada. Ejemplo: Si la entrada es A, la expresión algebraica sería ~A.

¿Para qué sirve la descripción algebraica?
La Descripción Algebraica de Circuitos Lógicos sirve para representar las operaciones y relaciones lógicas dentro de un sistema digital mediante expresiones algebraicas. Aquí se detallan sus propósitos y aplicaciones principales:
- Diseño de Circuitos Lógicos: La descripción algebraica es esencial en la fase de diseño de circuitos lógicos. Permite expresar las funciones lógicas del circuito en términos de operaciones algebraicas, facilitando la creación y especificación de la lógica subyacente.
- Análisis y Verificación: Se utiliza para analizar y verificar el comportamiento lógico de un circuito. Al representar las funciones lógicas mediante expresiones algebraicas, se pueden realizar análisis detallados para asegurarse de que el circuito cumple con los requisitos y especificaciones.
- Optimización de Circuitos: Facilita la optimización de circuitos lógicos. La simplificación algebraica de las expresiones booleanas puede llevar a una implementación más eficiente, reduciendo el número de compuertas y mejorando el rendimiento.
- Simulación y Modelado: En entornos de simulación, la descripción algebraica se utiliza para modelar el comportamiento de un circuito antes de su implementación física. Esto permite realizar pruebas virtuales y ajustes en el diseño sin la necesidad de construir prototipos físicos.
- Programación de Dispositivos Programables: Se emplea en la programación de dispositivos lógicos programables, como FPGAs y CPLDs. En lenguajes de descripción de hardware (HDL) como VHDL y Verilog, la descripción algebraica se traduce en lógica digital programable.
Ejemplo Práctico
Supongamos que queremos diseñar un circuito lógico que active una alarma (salida Y) si la puerta (entrada A) está cerrada y al menos una de las ventanas (entrada B o C) está abierta.
- A : Estado de la puerta (0 = abierta, 1 = cerrada).
- B : Estado de la ventana 1 (0 = abierta, 1 = cerrada).
- C : Estado de la ventana 2 (0 = abierta, 1 = cerrada).
- Y : Salida de la alarma (1 = activada, 0 = desactivada).
Desarrollo Paso a Paso:
1. Expresiones Lógicas:
Las expresiones lógicas se crean con el objetivo de representar y manipular el comportamiento de sistemas basados en lógica booleana. Estas expresiones son fundamentales en el diseño y análisis de circuitos lógicos y sistemas digitales, a continuación creamos una condición para tres escenarios:
- Condición para la puerta cerrada: Se puede utilizar también A’ para indicar el inverso de la entrada A.
- Condición para al menos una ventana abierta:
Babierta= B +C
- Condición para activar la alarma:
Y=Acerrada ⋅ Babierta
2. Descripción Algebraica:
La Descripción Algebraica en el contexto de circuitos lógicos se crea con varios propósitos clave, todos centrados en la representación y manipulación formal de la lógica booleana subyacente en estos sistemas. Partiendo de esta comprensión, procedemos a combinar las condiciones previamente mencionadas para determinar la salida del sistema de alarma.
Combinamos las condiciones utilizando la compuerta AND:
3. Tabla de verdad:
Construimos una tabla de verdad para verificar las condiciones y la salida de la alarma.
| A | B | C | A’ | B + C | Y |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
4. Implementación con Compuertas:
Cuando se menciona «implementación con compuertas», se está hablando de la utilización de estas compuertas para construir nuestro circuito para que realice la función especifica con las condiciones establecidas y cumpla con nuestra tabla de verdad.
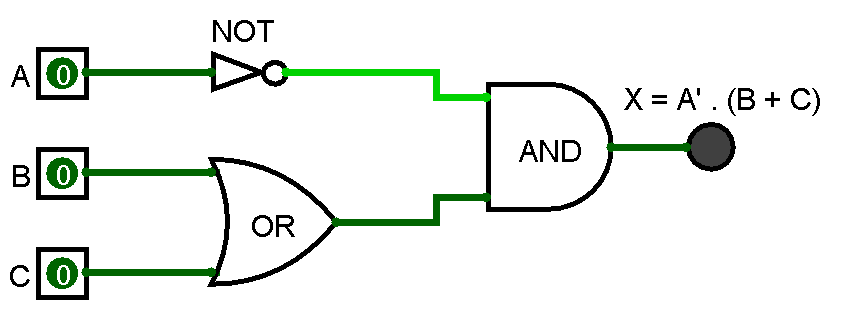
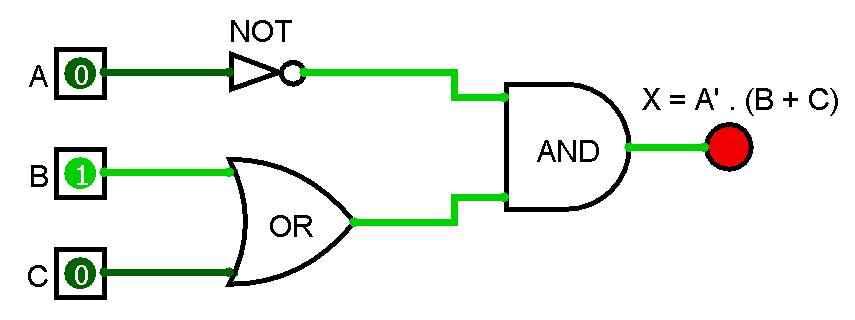
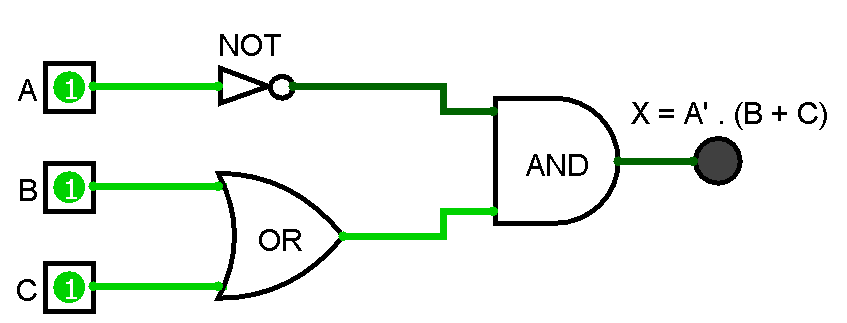
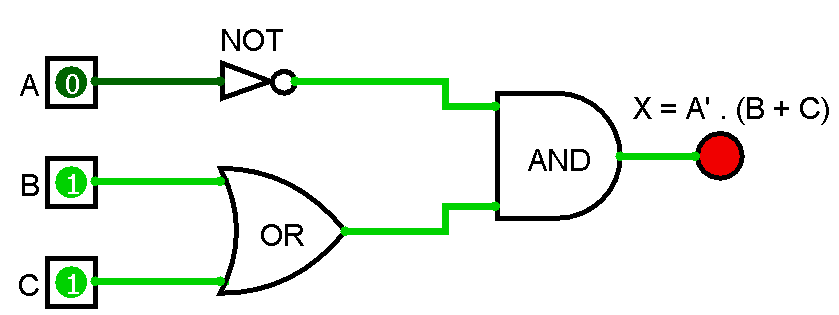
5. Diagrama del Circuito:
Ahora vamos a representa gráficamente la estructura y conexión de los componentes eléctricos de este circuito. Representamos el circuito lógico con las compuertas AND, OR y NOT conectadas según nuestras expresiones algebraicas.
Ventajas
La descripción algebraica de circuitos lógicos ofrece varias ventajas significativas en el diseño, análisis y optimización de sistemas digitales. Aquí hay algunas de las principales ventajas:
- Claridad y Concisión: Las expresiones algebraicas proporcionan una representación clara y concisa de las funciones lógicas. Esta claridad facilita la comprensión del comportamiento del circuito y su diseño.
- Facilidad de Manipulación: Las expresiones algebraicas son fáciles de manipular y simplificar mediante reglas algebraicas y de álgebra booleana. Esto facilita la optimización y reducción de funciones lógicas complejas.
- Síntesis y Optimización Eficiente: Permite la síntesis eficiente de funciones lógicas y su optimización. La simplificación algebraica ayuda a minimizar el número de compuertas lógicas y, por lo tanto, mejora la eficiencia en términos de recursos y velocidad.
- Análisis de Circuitos Complejos: Facilita el análisis de circuitos complejos al proporcionar una representación matemática que permite seguir y entender las relaciones lógicas entre las variables de entrada y salida.
- Documentación Estandarizada: Proporciona una forma estandarizada de documentar el diseño de circuitos lógicos. Esto facilita la comunicación entre diseñadores, ingenieros y otros profesionales, ya que todos pueden interpretar las expresiones algebraicas de manera consistente.
Conclusión
La descripción algebraica se erige como la piedra angular en el diseño y análisis de sistemas digitales, ofreciendo una representación matemática precisa y eficiente de las complejas funciones lógicas. Su capacidad para proporcionar claridad, facilidad de manipulación, optimización eficiente y una base sólida para la síntesis y simulación, consolida su importancia como una herramienta esencial en la ingeniería electrónica, permitiendo a los diseñadores lograr circuitos más eficientes y comprensibles.
Preguntas Frecuentes
Invita a otros a explorar: Comparte Ahora 📢