Mapas de Karnaugh: Simplificación Lógica Fácil y Rápida

En el mundo de la electrónica y telecomunicaciones, los Mapas de Karnaugh se han convertido en una herramienta esencial para simplificar circuitos lógicos. Diseñados para hacer más eficiente la minimización de expresiones booleanas, estos mapas gráficos permiten que cualquier persona, sin necesidad de ser un experto, pueda optimizar circuitos y ahorrar costos en el diseño de hardware. En esta guía, exploraremos qué son los ¿Qué es el Mapa de Karnaugh?, cómo se utilizan y por qué son tan importantes en el diseño de circuitos digitales.

¿Qué es el Mapa de Karnaugh?

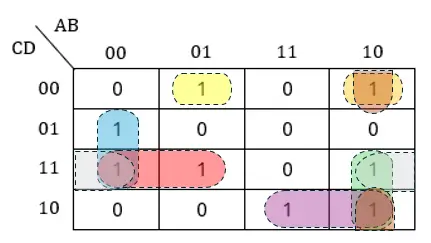
Los Mapas de Karnaugh, también llamados «K-maps», son una representación gráfica utilizada para simplificar expresiones booleanas en el diseño de circuitos lógicos digitales. Funcionan organizando las diferentes combinaciones de variables en un formato que facilita la identificación de patrones, los cuales, a su vez, permiten reducir complejas ecuaciones booleanas a su forma más simple.

Breve reseña histórica

Este método fue desarrollado por el ingeniero británico Maurice Karnaugh en la década de 1950 mientras trabajaba en Bell Labs. Su objetivo era simplificar la manipulación del álgebra de Boole, que ya era ampliamente utilizada en la electrónica digital.

¿Para qué se utilizan el Mapa de Karnaugh??

Los Mapas de Karnaugh se utilizan principalmente para:

• Simplificación de expresiones booleanas: Se pueden reducir ecuaciones lógicas complejas a su forma más simple.
• Diseño de circuitos lógicos: Optimiza los circuitos para que utilicen menos componentes.

Estas dos aplicaciones son fundamentales en el diseño de hardware digital, ya que permiten construir circuitos que sean más pequeños, rápidos y eficientes.

¿Cómo se construye un mapa de Karnaugh?

Para construir un Mapa de Karnaugh, es esencial entender cómo organizar las combinaciones de variables en una cuadrícula que permita identificar los grupos que simplificarán la expresión.

Número de variables de entrada y su representación

Dependiendo de la cantidad de variables en una función booleana, el Mapa de Karnaugh tendrá más o menos celdas. Cada celda representa una combinación posible de las variables.

• 2 variables: Un mapa de 2 variables tendrá 4 celdas (representando las combinaciones de y ).
• 3 variables: Un mapa de 3 variables tendrá 8 celdas, representando combinaciones de , y .

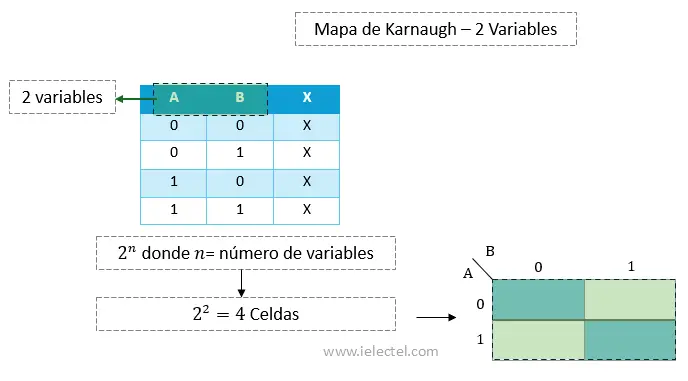
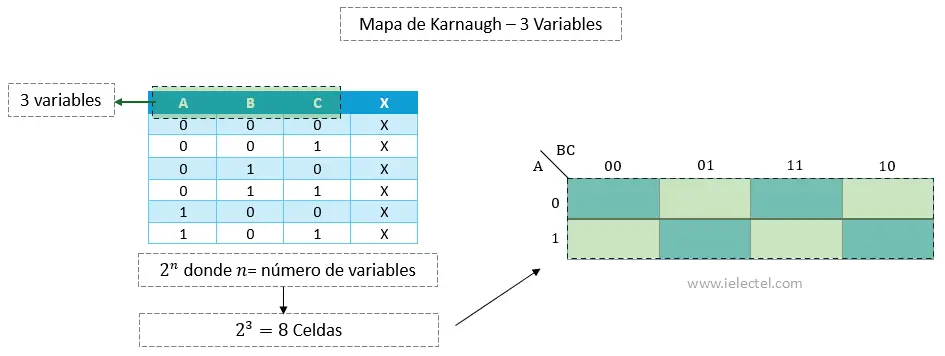
Llenado del Mapa

Para llenar el Mapa de Karnaugh utilizando la tabla de verdad de 2 variables, debemos asignar un 1 en las celdas donde la salida sea verdadera (1), y un 0 en las celdas donde la salida sea falsa (0).

1. Identifica los valores de la tabla de verdad:
   • Cuando y , la salida es .
   • Cuando y , la salida es .
   • Cuando y , la salida es .
   • Cuando y , la salida es .
2. Transfiere estos valores al Mapa de Karnaugh:
   • Asigna un 1 a la celda que corresponde a , .
   • Asigna un 0 a la celda de , .
   • Asigna un 0 a la celda de , .
   • Asigna un 1 a la celda de , .

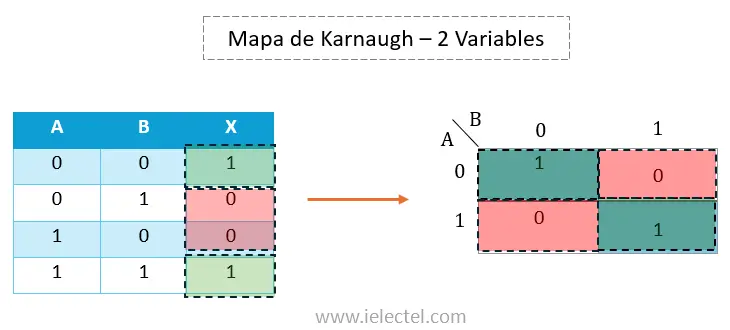
Este proceso nos permite crear una representación gráfica más clara de la función booleana, facilitando la simplificación de la expresión lógica.

Reglas de agrupamiento

1. Los grupos deben tener tamaños de potencia de 2

Los grupos que se formen en el Mapa de Karnaugh deben tener siempre un tamaño que sea una potencia de 2. Es decir, los grupos pueden tener 1, 2, 4, 8, 16, etc. celdas. No se permiten grupos con un número impar de celdas o cantidades que no correspondan a potencias de 2.

Ejemplos de agrupamiento permitido:

• Grupo de 1 celda
• Grupo de 2 celdas
• Grupo de 4 celdas
• Grupo de 8 celdas, y así sucesivamente.

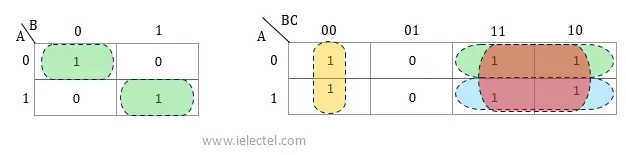
2. Celdas adyacentes deben contener el mismo valor

Para que dos o más celdas puedan agruparse, deben tener el mismo valor en el mapa. Por lo general, estamos interesados en agrupar celdas con valor 1 cuando buscamos una expresión booleana simplificada.

3. La adyacencia puede ser horizontal, vertical o envolvente

La adyacencia en los Mapas de Karnaugh es clave para formar grupos. Dos celdas son adyacentes si están directamente conectadas en sentido horizontal o vertical, pero también puede haber adyacencia entre extremos opuestos de la cuadrícula, lo que se conoce como adyacencia envolvente o toroidal.

• Horizontalmente adyacentes: Celdas una al lado de la otra en la misma fila.
• Verticalmente adyacentes: Celdas en la misma columna, una sobre la otra.
• Envolvente: Celdas en los bordes opuestos del mapa son adyacentes. Por ejemplo, en un mapa de 3 variables, las celdas en el borde izquierdo son adyacentes a las celdas del borde derecho.

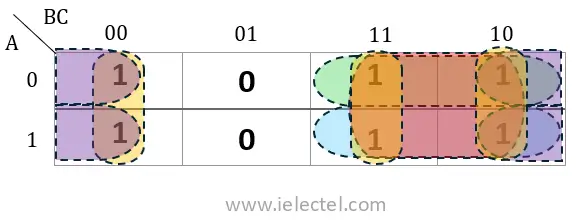
Esta adyacencia envolvente es fundamental, ya que permite agrupar términos aparentemente distantes en el mapa, lo que resulta en expresiones booleanas más simplificadas.

4. Los grupos deben ser lo más grandes posible

Una de las reglas más importantes en el agrupamiento de los Mapas de Karnaugh es que los grupos formados deben ser lo más grandes posibles. Cuanto mayor sea el grupo, mayor será la simplificación de la expresión booleana. Siempre que sea posible, agrupa el máximo número de celdas adyacentes en una sola agrupación.

Por ejemplo:

• Si puedes agrupar 4 celdas, en lugar de agrupar 2 y luego otras 2, siempre es preferible crear un grupo de 4.
• Los grupos grandes eliminan más variables de la expresión booleana, lo que da como resultado una ecuación más sencilla.

5. Cada celda con 1 debe ser parte de al menos un grupo

Todas las celdas que contienen un 1 deben incluirse en al menos un grupo. Sin embargo, una celda puede ser parte de varios grupos diferentes si esto contribuye a una mayor simplificación de la función.

Esto significa que se puede reutilizar una celda con un 1 en varios grupos si con ello se obtienen grupos más grandes o más simples. Esta técnica es útil para generar la simplificación óptima.

Generación de la Expresión Simplificada

Para simplificar la expresión booleana usando el Mapa de Karnaugh que has proporcionado, sigue los siguientes pasos detallados:

Agrupa las celdas con valor 1

El siguiente paso es identificar las celdas que contienen el valor 1 en el mapa para el ejemplo con 2 variables. En este caso, las celdas con valor 1 están en las siguientes posiciones:

• , →
• , →

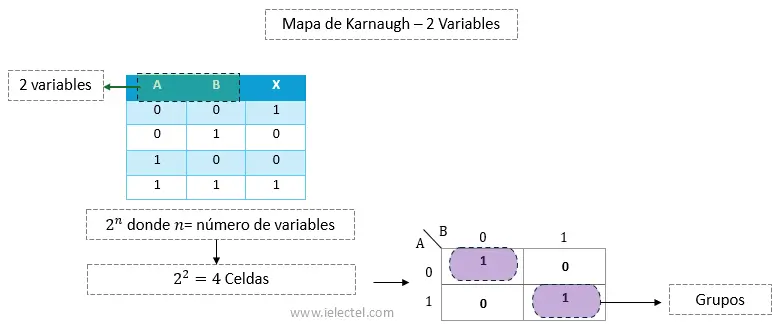
No es posible agrupar estas celdas en un solo grupo grande, ya que no son adyacentes entre sí. Por lo tanto, tendremos dos grupos de una sola celda.

Deriva los términos booleanos para cada grupo

Ahora, debemos escribir la expresión booleana para cada uno de los grupos (celdas con 1):

Grupo 1: ,

• Para esta celda, tanto como son 0.
• La variable es 0, lo que se representa como (negación de ).
• La variable es 0, lo que se representa como (negación de ).
• Por lo tanto, el término booleano para este grupo es .

Grupo 2: ,

• Para esta celda, tanto como son 1.
• La variable es 1, lo que se representa simplemente como .
• La variable es 1, lo que se representa simplemente como .
• Por lo tanto, el término booleano para este grupo es .

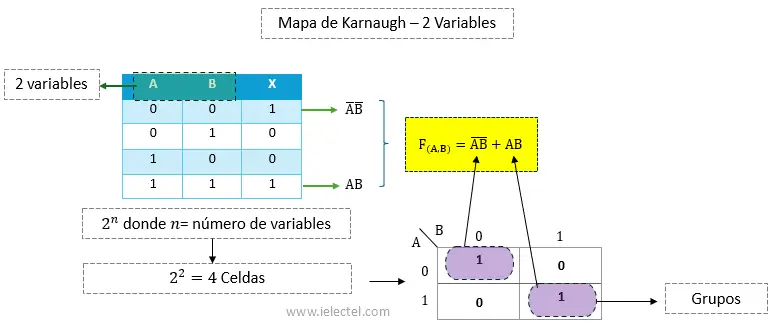
Escribe la expresión booleana final

Finalmente, la expresión booleana simplificada es la suma lógica (OR) de los términos obtenidos de los grupos formados. Sumamos los términos y para obtener la expresión final:

Ventajas del Mapa de Karnaugh

1. Método gráfico e intuitivo: Permite simplificar funciones booleanas de forma visual, haciendo más fácil la comprensión para usuarios.
2. Reducción de términos lógicos: Minimiza expresiones booleanas, reduciendo el número de compuertas necesarias en un circuito.
3. Identificación de redundancias: Facilita la eliminación de términos innecesarios, optimizando el diseño lógico.
4. Ahorro de tiempo: Permite simplificaciones rápidas en comparación con métodos algebraicos más complicados.
5. Uso didáctico: Ideal para aprender y enseñar conceptos básicos de lógica booleana y circuitos digitales.

Limitaciones del Mapa de Karnaugh

1. Limitado a pocas variables: Se vuelve difícil de manejar y visualizar con más de 4 o 5 variables.
2. Errores manuales: La construcción y agrupación manual puede generar errores, especialmente en mapas más complejos.
3. No siempre óptimo: En algunos casos, no proporciona la simplificación mínima más eficiente en comparación con otros métodos.
4. Complejidad con muchos términos: Mapas grandes son difíciles de leer y organizar correctamente.
5. Poca escalabilidad: Aunque efectivo para pocas variables, no es práctico para sistemas complejos sin el uso de software especializado.

Conclusión

El Mapa de Karnaugh es una herramienta fundamental para la simplificación de funciones booleanas en el ámbito de la electrónica digital y el diseño de circuitos lógicos. Su enfoque gráfico e intuitivo permite visualizar de manera clara las combinaciones de variables que generan salidas verdaderas, facilitando la eliminación de redundancias y la reducción de términos en una expresión lógica. Esto se traduce en una optimización de circuitos, ya que reduce el número de compuertas necesarias, disminuye el consumo de energía y mejora la eficiencia general del sistema.

Una de las principales ventajas de los Mapas de Karnaugh es su simplicidad y su capacidad de mostrar adyacencias entre términos que no son fácilmente visibles en otros métodos, como el álgebra de Boole o las tablas de verdad. Además, los mapas permiten la agrupación de términos en potencias de dos, lo que simplifica enormemente el diseño lógico.

Sin embargo, también presentan limitaciones. A medida que aumenta el número de variables, los mapas se vuelven más complejos y difíciles de manejar. En estos casos, los diseñadores suelen recurrir a herramientas automatizadas de software que extienden las capacidades de los Mapas de Karnaugh para un mayor número de variables.

En conclusión, el Mapa de Karnaugh sigue siendo una herramienta poderosa y esencial para los estudiantes y profesionales de la electrónica y las telecomunicaciones, ya que permite la optimización de circuitos de forma manual y visual, siendo un paso fundamental en el desarrollo de sistemas digitales eficientes.

Preguntas Frecuentes

¡Esperamos sinceramente que este post, repleto de contenido valioso, haya sido excepcionalmente útil en tu emocionante travesía hacia el fascinante mundo de la electrónica! 🌟 Te extendemos la invitación a explorar muchos más artículos, proyectos, contenido sobre equipos, software y más en nuestra página web.

Invita a otros a explorar: Comparte Ahora 📢