Sistemas Numéricos Digitales 🔢
En el ámbito de la tecnología digital, se emplean diversos sistemas numéricos digitales, siendo los más prevalentes el decimal, binario, octal y hexadecimal. Indiscutiblemente, el sistema decimal destaca como el más familiar, dado su uso cotidiano. Realicemos un análisis detenido de sus atributos con el propósito de profundizar en la comprensión de los sistemas numéricos.
¿Qué son los Sistemas Numéricos Digitales?
Los sistemas numéricos digitales son un método de representar valores numéricos mediante combinaciones de dígitos binarios, 0 y 1. En electrónica y computación, estos sistemas son fundamentales para el procesamiento de información. Cada posición en el número binario tiene un valor que es una potencia de 2. Estos sistemas son la base del lenguaje de las computadoras y son esenciales para la representación y manipulación eficiente de datos en el ámbito de la tecnología digital. La capacidad de convertir información en forma binaria permite el almacenamiento, procesamiento y transmisión eficaz de datos en dispositivos electrónicos y sistemas computacionales.
Sistema Decimal
El sistema decimal, base 10, es el sistema numérico más utilizado en la vida diaria y se compone de diez dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Cada posición en un número decimal tiene un valor que es una potencia de diez, y la posición más a la derecha representa las unidades. Al avanzar hacia la izquierda, cada posición sucesiva se multiplica por diez.

Ejemplo:
- Número Decimal Básico:
- Ejemplo: 3,257
- Desglose: 3×103 (3000) + 2×102 (200) + 5×101 (50) + 7×100 (7)
- Significado: Tres mil doscientos cincuenta y siete.
El sistema decimal, arraigado en la base de diez, proporciona una representación eficiente y ampliamente comprensible de cantidades, facilitando operaciones matemáticas y la expresión de valores en diversos contextos.
Sistema Binario
El sistema binario es un sistema numérico fundamental en la computación y la electrónica, caracterizado por su base 2, lo que implica el uso de solo dos dígitos: 0 y 1. A diferencia del sistema decimal que emplea diez dígitos, el binario simplifica la representación de información utilizando únicamente estas dos cifras. Cada posición en un número binario representa una potencia de dos, comenzando desde la derecha con 20 y duplicándose a medida que avanzamos hacia la izquierda.
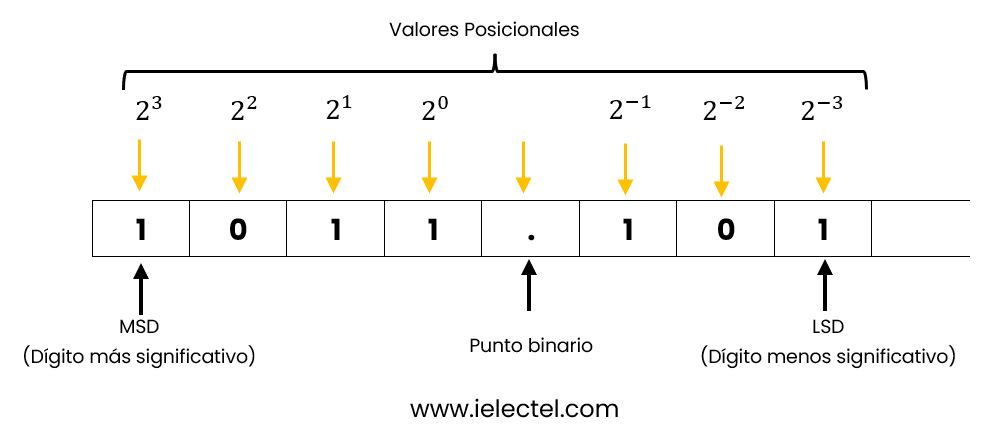
Ejemplo:
- Número Binario :
- Ejemplo: 1101
- Desglose:
- La posición más a la derecha representa 20 = 1.
- La siguiente posición hacia la izquierda representa 21 = 2.
- La siguiente posición representa 22 = 4.
- La posición más a la izquierda representa 23 = 8.
- Significado: Sumando estos valores, el número binario (1101) se traduce al sistema decimal como (8 + 4 + 0 + 1 = 13).
El sistema binario es esencial en la lógica de la computación, donde los dígitos 0 y 1 representan los estados de apagado y encendido, respectivamente. Se utiliza ampliamente en la representación de datos, la programación de computadoras y la comunicación digital, ofreciendo una base eficiente para el procesamiento de información en el ámbito tecnológico.
Sistema Hexadecimal
El sistema hexadecimal es un sistema de numeración que utiliza 16 dígitos, que van desde 0 hasta 9 y luego de A a F, donde A representa el valor 10 y F el valor 15. Es ampliamente utilizado en informática y programación debido a su conveniencia para representar valores binarios de manera más compacta. Cada dígito hexadecimal representa cuatro bits, facilitando la conversión entre binario y hexadecimal. Además, el sistema hexadecimal es utilizado para expresar direcciones de memoria y colores en la programación informática.
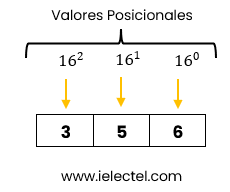
Tabla de Conversión: Decimales, Hexadecimales y Binarios (0-15)
| Decimal | Hexadecimal | Binario |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |


