/ Compuertas Lógicas, Electrónica digital / Por

Teorema de DeMorgan: Principios Básicos y Aplicaciones

Tabla de contenidos
  1. Teorema de DeMorgan: Principios Básicos y Aplicaciones

El Teorema de DeMorgan es una de las herramientas más fundamentales y útiles en el ámbito de la electrónica digital y las telecomunicaciones. Este teorema ofrece una manera simplificada de trabajar con expresiones lógicas complejas, permitiendo transformar funciones lógicas para facilitar su análisis y diseño. En este artículo titulado Teorema de DeMorgan: Principios Básicos y Aplicaciones. vamos a explorar de manera detallada y clara todo lo relacionado con este teorema, desde sus bases teóricas hasta sus aplicaciones prácticas, de una manera sencilla para que cualquiera pueda comprenderlo y aplicarlo en sus estudios o proyectos. ¡Así que empecemos!

¿Qué es el Teorema de DeMorgan?

El Teorema de DeMorgan es una ley en el álgebra booleana, nombrada así en honor al matemático y lógico británico Augustus De Morgan. Este teorema describe cómo los operadores lógicos AND y OR se relacionan entre sí a través de la negación (NOT).

En palabras simples, el teorema tiene dos reglas fundamentales que se aplican a expresiones lógicas:

  • Regla N° 1.- Cuando se invierte la suma lógica (OR) de dos variables, es equivalente a invertir cada variable individualmente y luego aplicar una operación AND (multiplicación lógica) entre las dos variables invertidas.

\overline{A + B} = \overline{A} \cdot \overline{B}

Teorema de DeMorgan: Principios Básicos y Aplicaciones.

  • Regla N° 2.- Cuando se invierte el producto lógico (AND) de dos variables, es equivalente a invertir cada variable individualmente y luego aplicar una operación OR (suma lógica) entre las dos variables negadas.

\overline{A \cdot B} = \overline{A} + \overline{B}

Teorema de DeMorgan: Principios Básicos y Aplicaciones.

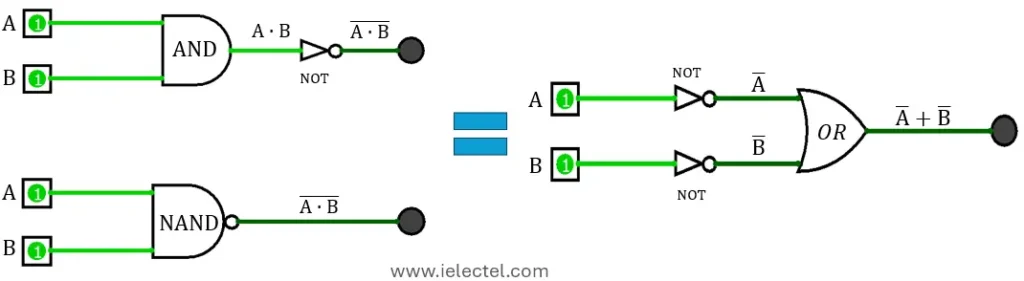
Estas reglas nos permiten simplificar y reescribir expresiones lógicas de una manera más manejable, lo que es especialmente útil en la minimización de circuitos lógicos.

¿Cómo se Aplica el Teorema de DeMorgan?

El Teorema de DeMorgan es crucial en el diseño de circuitos digitales. En electrónica, trabajamos frecuentemente con puertas lógicas, como las puertas AND, OR, y NOT. Estas puertas forman el corazón de los sistemas digitales, como los procesadores y las memorias.

El teorema permite transformar puertas lógicas complejas en otras más simples o en combinaciones más fáciles de implementar en circuitos reales. Por ejemplo:

  • Un circuito AND puede convertirse en un circuito equivalente que use puertas OR y NOT, gracias al teorema.
  • Del mismo modo, una puerta OR puede reescribirse en términos de AND y NOT, facilitando su diseño.

Esto no solo ayuda a simplificar el diseño, sino que también optimiza el consumo de energía y el rendimiento del circuito, algo esencial en el mundo de las telecomunicaciones y los dispositivos electrónicos modernos.

Ejemplo Práctico

Como ejemplo práctico donde se puede aplicar el Teorema de DeMorgan tenemos:

  • Determina la expresión lógica de salida para el circuito mostrado en la siguiente figura y simplifícala.
Teorema de DeMorgan: Principios Básicos y Aplicaciones.

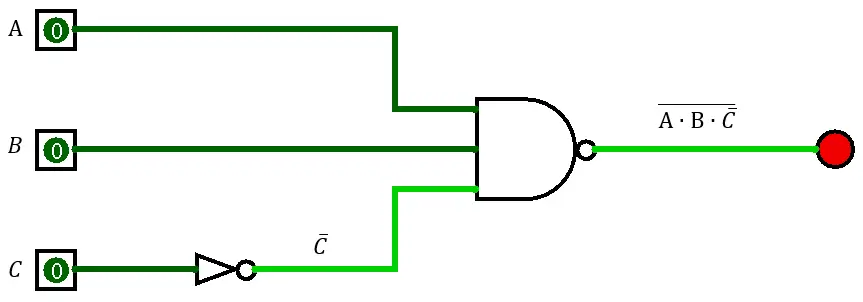
Para detallar mejor el proceso, descompondremos cada parte del circuito y usaremos los teoremas de DeMorgan paso a paso. Vamos a desglosar la imagen del circuito:

Paso 1: Identificar las compuertas y las entradas

  • El circuito tiene tres entradas: A, B y C.
  • La entrada C pasa por una compuerta NOT, lo que convierte C en \overline{C}.
  • Las tres entradas A, B, y \overline{C} luego se combinan en una compuerta AND, lo que produce:

A\cdot B \cdot \overline{C}

Esta es la salida de la compuerta AND.

  • Después, esta salida pasa por una compuerta NOT final, que invierte el resultado. Esto nos da:

z = \overline{A \cdot B \cdot \overline{C}}

Esta es la primera expresión de la salida z.

Es importante tener en cuenta que, al negar una compuerta AND, podemos utilizar una compuerta NAND para lograr el mismo efecto, tal como se ilustra en la figura.

Paso 2: Aplicar el Teorema de DeMorgan

El teorema de DeMorgan se usa para transformar la negación de una conjunción (AND) en una disyunción (OR). En este caso, tenemos que:

z = \overline{A \cdot B \cdot \overline{C}}

Según la Regla N° 2 del teorema de DeMorgan, podemos transformar la negación de un AND de la siguiente manera:

\overline{A \cdot B \cdot C} = \overline{A} + \overline{B} + \overline{C}

Aplicamos este teorema a la expresión anterior, teniendo en cuenta que ya tenemos \overline{C}, así que debemos invertirlo de nuevo:

z = \overline{A} + \overline{B} + C

Este es el resultado simplificado.

Paso 3: Verificación de la expresión

La salida z ahora se ha transformado a:

z = \overline{A} + \overline{B} + C

Esto significa que:

  • z será 1 si A es 0, o si B es 0, o si C es 1.
  • Es una función OR de \overline{A}, \overline{B} y C.

Este es el comportamiento lógico completo del circuito y la expresión final para la salida.

Teorema de DeMorgan: Principios Básicos y Aplicaciones.

Importancia del Teorema de DeMorgan

El Teorema de DeMorgan tiene implicaciones directas en el diseño y simplificación de circuitos digitales. A menudo, en la etapa de diseño, es necesario optimizar los circuitos tanto en términos de costo (minimizar el número de puertas lógicas) como de eficiencia (reducir el tiempo de procesamiento y el consumo de energía).

Por ejemplo, el uso de puertas NAND y NOR es muy común debido a que son más baratas y fáciles de implementar en hardware. Gracias al Teorema de DeMorgan, podemos convertir casi cualquier circuito en uno que solo use estas puertas, logrando un diseño más eficiente y económico.

Aplicaciones del Teorema de DeMorgan

El Teorema de DeMorgan tiene múltiples aplicaciones en distintos campos, principalmente en la electrónica, telecomunicaciones, y la informática. A continuación, se detallan algunas de sus principales aplicaciones:

1. Diseño de Circuitos Digitales

Uno de los usos más comunes del Teorema de DeMorgan es en el diseño y simplificación de circuitos digitales. Al aplicar este teorema, los ingenieros pueden transformar expresiones lógicas complejas, facilitando la reducción del número de puertas lógicas necesarias en un circuito.

  • Simplificación de circuitos: Convertir puertas AND en combinaciones de OR y NOT (y viceversa) puede reducir los componentes de un circuito.
  • Minimización de costos y energía: Menos puertas lógicas implican menores costos de fabricación y menor consumo energético, lo que es vital para dispositivos electrónicos que operan con batería.

2. Implementación con Puertas NAND y NOR

Las puertas NAND y NOR son muy comunes en la fabricación de circuitos digitales debido a que son más baratas y versátiles. Usando el Teorema de DeMorgan, se pueden transformar prácticamente todas las expresiones lógicas para que utilicen solo puertas NAND o NOR, lo que simplifica el proceso de fabricación.

  • Circuitos NAND/NOR-only: Este enfoque es particularmente útil en sistemas donde las puertas NAND y NOR son las más eficientes en términos de tiempo de operación y costo.

3. Optimización de Algoritmos Lógicos en Programación

En la programación, especialmente en la lógica booleana, el Teorema de DeMorgan es clave para simplificar condiciones lógicas complejas. Esto mejora tanto la legibilidad del código como la eficiencia del algoritmo.

  • Simplificación de condiciones lógicas: El Teorema de DeMorgan permite reescribir condiciones que involucren AND y OR con negaciones, lo que puede hacer que el código sea más claro y fácil de seguir.
  • Optimización de código: Al simplificar la lógica en operaciones booleanas, se mejora el rendimiento del programa al reducir la cantidad de cálculos lógicos innecesarios.

4. Diseño de Sistemas de Control

En sistemas de control digital, como semáforos o sistemas de seguridad, el Teorema de DeMorgan ayuda a diseñar lógicas de control que dependen de sensores.

  • Ejemplo: En un sistema de seguridad con varios sensores (puertas, ventanas, movimiento), el Teorema de DeMorgan facilita el diseño de la lógica que activa una alarma solo cuando ninguna condición de alerta es verdadera.

5. Procesadores y Arquitectura de Computadoras

Los procesadores y las unidades lógicas aritméticas (ALU) hacen uso intensivo de puertas lógicas. El Teorema de DeMorgan permite simplificar las operaciones lógicas en estos circuitos, lo que puede resultar en arquitecturas más eficientes.

  • Minimización del hardware: En la implementación de operaciones booleanas a nivel de hardware, el uso del teorema puede reducir el número de puertas requeridas en un procesador.

6. Redes de Telecomunicaciones

En redes digitales de telecomunicaciones, donde la transmisión de datos es crítica, las operaciones lógicas que optimizan la decodificación de señales son fundamentales. El Teorema de DeMorgan permite diseñar sistemas de procesamiento de señales que operen de manera eficiente.

  • Filtrado y codificación de datos: Las expresiones lógicas simplificadas pueden hacer que el filtrado de datos en redes de alta velocidad sea más rápido y consuma menos recursos.

7. Sistemas de Inteligencia Artificial y Toma de Decisiones

En la lógica difusa o los sistemas de inteligencia artificial, las decisiones basadas en reglas se benefician de las simplificaciones lógicas que el Teorema de DeMorgan ofrece.

  • Mejora en la toma de decisiones: Los sistemas de IA que operan sobre reglas lógicas pueden procesar las entradas de forma más eficiente, utilizando expresiones booleanas simplificadas.

El Teorema de DeMorgan es una herramienta invaluable para simplificar tanto circuitos físicos como expresiones lógicas en diferentes dominios. Esto no solo optimiza el diseño y la implementación de sistemas, sino que también mejora el rendimiento y reduce costos, haciéndolo esencial en el mundo de la electrónica, informática, y telecomunicaciones.

Ejercicio Práctico

Construye un circuito lógico en un protoboard que represente la siguiente expresión:

Teorema de DeMorgan: Principios Básicos y Aplicaciones.

z = \overline{(A + B)} \cdot \overline{(B \cdot C)}

Luego, simplifica el circuito aplicando el Teorema de DeMorgan y verifica la equivalencia entre el circuito original y su versión simplificada.

Teorema de DeMorgan: Principios Básicos y Aplicaciones.

Pasos para resolver el ejercicio:

1. Circuito lógico original

El objetivo es implementar la siguiente expresión:

z = \overline{(A + B)} \cdot \overline{(B \cdot C)}

Esto involucra los siguientes pasos:

  1. Primera parte del circuito:
    • Usa una compuerta OR para sumar las entradas A y B. Esto te dará A + B
    • Pasa el resultado de la compuerta OR a una compuerta NOT para obtener ‾\overline{(A + B)}​.
  2. Segunda parte del circuito:
    • Usa una compuerta AND para multiplicar B y C, obteniendo B \cdot C.
    • Pasa el resultado de la compuerta AND a una compuerta NOT para obtener ‾\overline{(B \cdot C)}.
  3. Tercera parte del circuito:
    • Usa una compuerta AND para multiplicar los resultados de las dos compuertas NOT anteriores: ‾\overline{(A + B)} y ‾\overline{(B \cdot C)}​, obteniendo finalmente la salida:

z = \overline{(A + B)} \cdot \overline{(B \cdot C)}

2. Aplicar el Teorema de DeMorgan:

Ahora, vamos a simplificar esta expresión usando el Teorema de DeMorgan.

  • El teorema de DeMorgan nos dice que:

\overline{(A + B)} = \overline{A} \cdot \overline{B}

y

\overline{(B \cdot C)} = \overline{B} + \overline{C}

Al aplicar estas transformaciones, la expresión se simplifica a:

z = (\overline{A} \cdot \overline{B}) \cdot (\overline{B} + \overline{C})

3. Circuito simplificado:

El nuevo circuito simplificado es:

  • Usa una compuerta NOT para A, obteniendo \overline{A}.
  • Usa una compuerta NOT para B, obteniendo \overline{B}.
  • Usa una compuerta NOT para C, obteniendo ‾\overline{C}.
  • Usa una compuerta AND para multiplicar \overline{A} y \overline{B}, obteniendo \overline{A} \cdot \overline{B}.
  • Usa una compuerta OR para sumar \overline{B} y \overline{C}, obteniendo \overline{B} + \overline{C}.
  • Finalmente, usa una compuerta AND para multiplicar los dos resultados anteriores, obteniendo:

    z = (\overline{A} \cdot \overline{B}) \cdot (\overline{B} + \overline{C})

    Vamos a intentar simplificarla aún más.

    Paso 1: Aplicar la propiedad distributiva

    Usaremos la propiedad distributiva del álgebra booleana. Esta propiedad nos dice que:

    X \cdot (Y + Z) = (X \cdot Y) + (X \cdot Z)

    Aplicamos esta propiedad a la expresión:

    z = (\overline{A} \cdot \overline{B}) \cdot (\overline{B} + \overline{C})

    Distribuimos \overline{A} \cdot \overline{B} sobre \overline{B} + \overline{C}:

    z = (\overline{A} \cdot \overline{B} \cdot \overline{B}) + (\overline{A} \cdot \overline{B} \cdot \overline{C})

    Paso 2: Simplificar términos redundantes

    Sabemos que \overline{B} \cdot \overline{B} = \overline{B}, así que la expresión se simplifica a:

    z = (\overline{A} \cdot \overline{B}) + (\overline{A} \cdot \overline{B} \cdot \overline{C})

    Ahora observamos que \overline{A} \cdot \overline{B} es un factor común en ambos términos, por lo que podemos factorizarlo:

    z = \overline{A} \cdot \overline{B} \cdot (1 + \overline{C})

    Paso 3: Simplificar usando identidades booleanas

    Sabemos que 1 + \overline{C} = 1, ya que cualquier valor OR con 1 siempre da 1 (según las identidades booleanas). Por lo tanto, la expresión se reduce a:

    z = \overline{A} \cdot \overline{B}

    Teorema de DeMorgan: Principios Básicos y Aplicaciones.

    • La salida z será 1 solo cuando A sea 0 y B sea 0. Es decir, es el AND de \overline{A} y \overline{B}.

    4. Montaje en el protoboard:

    El circuito simplificado ahora requiere:

    • Dos compuertas NOT (para obtener \overline{A} y \overline{B}).
    • Una compuerta AND para multiplicar \overline{A} y \overline{B}.
    Teorema de DeMorgan: Principios Básicos y Aplicaciones.

    De esta forma, el circuito es más simple y eficiente de implementar.

    Hemos preparado para ti en Tinkercad una demostración visual de cómo el Teorema de DeMorgan simplifica el circuito. Podrás comparar el comportamiento del circuito original con el optimizado.

    Ventajas de Utilizar el Teorema de DeMorgan

    1. Simplificación de circuitos: Reduce la cantidad de puertas lógicas necesarias en un circuito.
    2. Mejora la eficiencia: Optimiza el tiempo de procesamiento y el consumo energético, crucial para dispositivos electrónicos modernos.
    3. Mayor flexibilidad en diseño: Permite transformar una configuración de puertas lógicas en otra equivalente, ofreciendo más opciones de diseño.
    4. Facilita la minimización booleana: Herramienta clave para simplificar expresiones booleanas.

    Conclusión

    El Teorema de DeMorgan es una herramienta vital para cualquier persona interesada en electrónica o telecomunicaciones. A través de este teorema, se pueden simplificar circuitos lógicos complejos y mejorar la eficiencia de los sistemas digitales, optimizando tanto el hardware como el software que maneja la información.

    Ya sea que estés diseñando circuitos, programando un microcontrolador o trabajando con redes de telecomunicaciones, dominar el Teorema de DeMorgan te dará una ventaja importante en la resolución de problemas complejos de manera más eficiente.

    Preguntas Frecuentes

    ¡Esperamos sinceramente que este post, repleto de contenido valioso, haya sido excepcionalmente útil en tu emocionante travesía hacia el fascinante mundo de la electrónica! 🌟 Te extendemos la invitación a explorar muchos más artículos, proyectos, contenido sobre equipos, software y más en nuestra página web.

    Invita a otros a explorar: Comparte Ahora 📢

    Entradas Relacionadas

    tablas de verdad

    Tablas de Verdad

    Tablas de Verdad en Electrónica 👨‍💻 Las tablas de verdad…

    Subscribe
    Subscribe
    Scroll al inicio