/ Conceptos Fundamentales, Electrónica, Electrónica Básica / Por

Cómo Realizar el Análisis de Mallas en Circuitos Eléctricos: Guía Básica

Tabla de contenidos
  1. ¿Qué es el Análisis de Mallas?
  2. ¿Qué es una malla en un circuito eléctrico?
  3. Pasos para Realizar el Análisis de Mallas
  4. Ventajas y Desventajas del Análisis de Mallas
  5. Consejos para Principiantes
  6. Conclusión
  7. Preguntas Frecuentes

Cuando se trata de resolver circuitos eléctricos complejos, existen varios métodos que se pueden utilizar. Uno de los más importantes es el análisis de mallas, un enfoque que simplifica considerablemente el cálculo de las corrientes en circuitos con múltiples ramas. En esta guía básica, te mostraré cómo realizar el análisis de mallas en circuitos eléctricos, explicando cada paso de manera clara y accesible para aquellos que recién se inician en el campo de la electrónica y las telecomunicaciones.

¿Qué es el Análisis de Mallas?

El análisis de mallas es un método utilizado para calcular las corrientes en un circuito eléctrico cerrado (malla), utilizando las leyes de Kirchhoff. Estas leyes son fundamentales en el análisis de cualquier circuito y se dividen en dos:

  1. Ley de Corrientes de Kirchhoff (LKC): Establece que la suma de las corrientes que entran a un nodo es igual a la suma de las corrientes que salen del nodo.
  2. Ley de Voltajes de Kirchhoff (LKV): Dice que la suma de todas las tensiones (voltajes) en un lazo cerrado debe ser igual a cero.

Estas dos leyes son la base del análisis de mallas. En términos simples, el análisis de mallas busca determinar cuánta corriente está circulando a través de cada componente en un circuito.

¿Qué es una malla en un circuito eléctrico?

Una malla en un circuito eléctrico es una trayectoria cerrada dentro del circuito por la que puede circular una corriente. Esta trayectoria no debe contener ningún otro lazo dentro de ella. En otras palabras, una malla es un camino cerrado que sigue por el circuito, pasando por diferentes componentes como resistencias o fuentes de voltaje, sin cruzarse o dividirse en otro camino cerrado.

Pasos para Realizar el Análisis de Mallas

Cómo Realizar el Análisis de Mallas en Circuitos Eléctricos

Para resolver este circuito utilizando el Análisis de Mallas, seguiremos un enfoque paso a paso, explicando cada cálculo y su justificación.

Paso 1: Identificación de las Mallas y Asignación de Corrientes

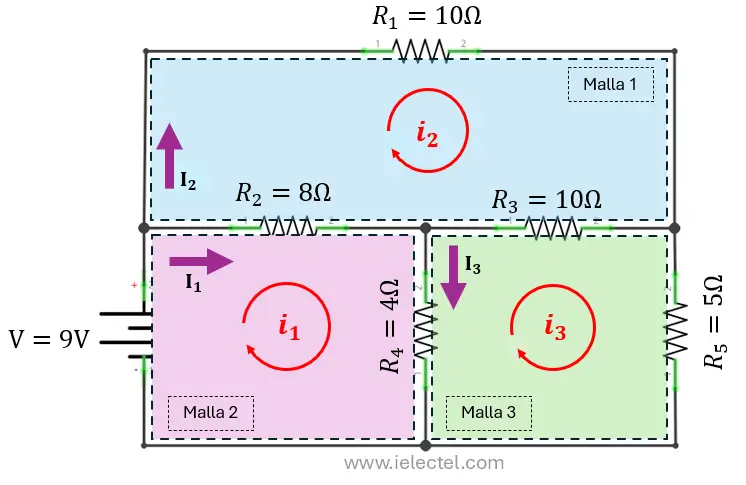
En la imagen proporcionada, tenemos un circuito con tres mallas:

  • Malla 1 (i₁): Contiene la fuente de voltaje V, la resistencia R_2​, y R_4​.
  • Malla 2 (i₂): Incluye las resistencias R_1​, R_3​, y comparte R_2​ con la Malla 1.
  • Malla 3 (i₃): Incluye las resistencias R_4​ y R_5​, compartiendo R_4​ con la Malla 1.

Ya que tenemos tres mallas, asignamos una corriente a cada una:

  • I_1 para la Malla 1.
  • I_2​ para la Malla 2.
  • I_3​ para la Malla 3.
Cómo Realizar el Análisis de Mallas en Circuitos Eléctricos

Paso 2: Aplicación de la Ley de Kirchhoff de Voltajes (LKV)

Para cada malla, aplicamos la Ley de Kirchhoff de Voltajes, que establece que la suma de todas las caídas y aumentos de voltaje en un lazo cerrado es igual a cero.

Malla 1 (i₁)

Recorremos la Malla 1 en sentido horario, encontrando las siguientes caídas de voltaje:

V - I_1 R_2 - I_1 R_4 - I_2 R_2 - I_3 R_4 = 0

Sustituyendo los valores de las resistencias y el voltaje:

9 - 8I_1 - 4I_1 - 8I_2 - 4I_3 = 0

Simplificando:

-12I_1 - 8I_2 - 4I_3 = -9

O:

12I_1 + 8I_2 + 4I_3 = 9 \quad \text{(Ecuación 1)}

Malla 2 (i₂)

En la Malla 2, también recorremos en sentido horario. La resistencia R_2​ es compartida con la Malla 1:

I_2 R_1 + I_2 R_3 + I_2 R_2 - I_1 R_2 = 0

Sustituyendo los valores de las resistencias:

10I_2 + 10I_2 + 8I_2 - 8I_1 = 0

Simplificando:

28I_2 - 8I_1 = 0 \quad \text{(Ecuación 2)}

Malla 3 (i₃)

En la Malla 3, recorremos en sentido horario. La resistencia R_4 es compartida con la Malla 1, por lo que restamos la corriente I_1:

I_3 R_4 + I_3 R_5 - I_1 R_4 = 0

Sustituyendo los valores de las resistencias:

4I_3 + 5I_3 - 4I_1 = 0

Simplificando:

9I_3 - 4I_1 = 0 \quad \text{(Ecuación 3)}

Paso 4: Resolución del Sistema de Ecuaciones

Tenemos el siguiente sistema de ecuaciones:

  1. 12I_1 + 8I_2 + 4I_3 = 9
  2. -8I_1 + 28I_2 = 0
  3. -4I_1 + 9I_3 = 0

Solución de la Ecuación 2 para I_2:

De la ecuación 2:

-8I_1 + 28I_2 = 0

Despejamos I_2​:

I_2 = \frac{8I_1}{28} = \frac{2I_1}{7}

Solución de la Ecuación 3 para I_3​:

De la ecuación 3:

-4I_1 + 9I_3 = 0

Despejamos I_3​:

I_3 = \frac{4I_1}{9}

Sustitución en la Ecuación 1:

Ahora sustituimos I_2​ e I_3​ en la ecuación 1:

12I_1 + 8\left(\frac{2I_1}{7}\right) + 4\left(\frac{4I_1}{9}\right) = 9

Simplificamos los términos:

12I_1 + \frac{16I_1}{7} + \frac{16I_1}{9} = 9

Multiplicamos todo por el mínimo común denominador (63) para eliminar los denominadores:

63(12I_1) + 63\left(\frac{16I_1}{7}\right) + 63\left(\frac{16I_1}{9}\right) = 63(9)

Lo que da:

756I_1 + 144I_1 + 112I_1 = 567

Simplificando:

1012I_1 = 567

Despejamos I_1​:

I_1 = \frac{567}{1012} \approx 0.56 \, \text{A}

Cálculo de I_2​ e I_3​:

Ahora que tenemos I_1​, podemos calcular I_2​ e I_3:

  • I_2 = \frac{2I_1}{7} = \frac{2 \times 0.56}{7} \approx 0.16 \, \text{A}
  • I_3 = \frac{4I_1}{9} = \frac{4 \times 0.56}{9} \approx 0.25 \, \text{A}

Paso 5: Verificación

Verificamos si las corrientes satisfacen las ecuaciones originales.

  1. 12I_1 + 8I_2 + 4I_3 = 9
    • 12(0.56) + 8(0.16) + 4(0.25) = 9
    • 6.72 + 1.28 + 1 = 9 ✔️
  2. -8I_1 + 28I_2 = 0
    • -8(0.56) + 28(0.16) = 0
    • -4.48 + 4.48 = 0 ✔️
  3. -4I_1 + 9I_3 = 0
    • -4(0.56) + 9(0.25) = 0
    • -2.24 + 2.25 \approx 0 ✔️

Ventajas y Desventajas del Análisis de Mallas

El análisis de mallas tiene varias ventajas, especialmente cuando se trata de circuitos con muchas componentes. A continuación, detallamos las ventajas y desventajas de utilizar este método:

Ventajas del Análisis de Mallas:

  • El análisis de mallas es muy eficiente cuando se trabaja con circuitos planos, es decir, aquellos que pueden ser dibujados sin que los conductores se crucen. Para estos tipos de circuitos, el número de ecuaciones a resolver es mínimo, lo que simplifica considerablemente el proceso de análisis.
  • A diferencia de otros métodos, como el análisis nodal, donde se utilizan ecuaciones de corrientes, en el análisis de mallas se trabaja con las corrientes de las mallas. Si se tiene un circuito con muchas ramas, el número de ecuaciones requeridas para el análisis por mallas suele ser menor que con el análisis nodal, lo que implica menos trabajo algebraico.
  • Este método permite visualizar el flujo de corriente de manera clara en cada malla del circuito, lo que es útil para entender cómo interactúan los distintos componentes en términos de voltaje y corriente.

Desventajas del Análisis de Mallas:

  • Aunque el número de ecuaciones es menor en comparación con otros métodos, los errores algebraicos, especialmente con signos y simplificaciones, pueden afectar los resultados finales. Estos errores son más comunes cuando se realizan cálculos manuales con ecuaciones simultáneas.
  • En circuitos con un gran número de mallas, el análisis puede generar muchas ecuaciones simultáneas, lo que aumenta el tiempo de cálculo y la probabilidad de errores. En estos casos, es más práctico usar programas de simulación como SPICE para resolver el circuito.
  • Si el circuito contiene elementos no lineales como diodos o transistores, el análisis de mallas pierde su simplicidad, ya que la relación corriente-voltaje no es lineal, lo que hace que el cálculo analítico sea más difícil.

Consejos para Principiantes

  • Familiarízate con la Ley de Ohm: Es esencial para comprender cómo se relacionan voltaje, corriente y resistencia.
  • Practica con ejemplos sencillos: Empieza con circuitos de dos mallas y luego avanza a configuraciones más complejas.
  • Verifica tus resultados: Siempre revisa que la suma de las corrientes y voltajes cumpla con las leyes de Kirchhoff.

Conclusión

El análisis de mallas es una herramienta valiosa en la electrónica y telecomunicaciones. Al dominar esta técnica, serás capaz de resolver circuitos eléctricos de manera eficiente y precisa. No importa si estás comenzando; con paciencia y práctica, puedes entender fácilmente los conceptos básicos. Sigue practicando con diferentes configuraciones de circuitos y recuerda que cada paso te acerca a un mayor dominio en el análisis de circuitos.

Preguntas Frecuentes

¡Esperamos sinceramente que este post, repleto de contenido valioso, haya sido excepcionalmente útil en tu emocionante travesía hacia el fascinante mundo de la electrónica! 🌟 Te extendemos la invitación a explorar muchos más artículos, proyectos, contenido sobre equipos, software y más en nuestra página web.

Invita a otros a explorar: Comparte Ahora 📢

Entradas Relacionadas

Subscribe
Subscribe
Scroll al inicio