/ Conceptos Fundamentales, Electrónica, Electrónica Básica / Por

¿Qué son las Leyes de Kirchhoff? – Fórmulas y Ejemplos Prácticos.

Tabla de contenidos
  1. ¿Qué son las Leyes de Kirchhoff?
  2. ¿Por qué son importantes las Leyes de Kirchhoff?
  3. Consejos para Principiantes
  4. Errores Comunes al Aplicar las Leyes de Kirchhoff
  5. Preguntas Frecuentes

Las Leyes de Kirchhoff son dos principios esenciales en el análisis de circuitos eléctricos, que nos permiten calcular de manera precisa los voltajes y corrientes en cualquier tipo de circuito, desde los más sencillos hasta los más complejos. Si estás iniciándote en el mundo de la electrónica o simplemente necesitas refrescar tus conocimientos, dominar estas leyes es fundamental para poder resolver y analizar redes eléctricas con mayor confianza. En esta guía, titulada ¿Qué son las Leyes de Kirchhoff, te explicaremos en detalle qué son estas leyes, sus fórmulas, y te proporcionaremos ejemplos prácticos para que puedas aprender a aplicarlas de manera clara y sencilla.

¿Qué son las Leyes de Kirchhoff?

Las leyes de Kirchhoff son como las reglas de tránsito para la electricidad en los circuitos. Sirven para analizar cómo se comporta la corriente y el voltaje en diferentes partes de un circuito eléctrico. El físico alemán Gustav Kirchhoff formuló dos leyes básicas que gobiernan el comportamiento de las corrientes y voltajes en un circuito eléctrico.

Ley de Kirchhoff de Corrientes (LKC)

La Ley de Kirchhoff de Corrientes (LKC), también conocida como la Primera Ley de Kirchhoff, establece que la suma de todas las corrientes que entran y salen de un nodo en un circuito eléctrico es igual a cero. Es decir, la cantidad de corriente que entra a un punto de conexión (nodo) debe ser igual a la cantidad de corriente que sale de él.

Conceptos Clave

  • Nodo: Un nodo es un punto en un circuito donde dos o más componentes están conectados. En un nodo, la corriente puede dividirse entre diferentes ramas del circuito.
¿Qué son las Leyes de Kirchhoff? - Fórmulas y Ejemplos Prácticos.

  • Corriente: Es el flujo de carga eléctrica a través de un conductor, generalmente medido en amperios (A). En un circuito, la corriente sigue un camino definido y puede dividirse o combinarse en nodos.
¿Qué son las Leyes de Kirchhoff? - Fórmulas y Ejemplos Prácticos.

  • Conservación de la carga: La LKC se basa en el principio de conservación de la carga, que dice que la carga eléctrica no puede acumularse en un nodo. Esto implica que la cantidad de corriente que entra a un nodo debe ser igual a la cantidad que sale.

Fórmula de la Ley de Kirchhoff de Corrientes

La expresión matemática de la LKC es la siguiente:

\sum I_{entrada} = \sum I_{salida}

Esto significa que si sumamos todas las corrientes que fluyen hacia el nodo y las que salen de él, el total será igual. Para hacer más fácil el uso de esta fórmula, consideramos que las corrientes que entran al nodo son positivas y las que salen del nodo son negativas.

Ejemplo de Aplicación de la LKC

¿Qué son las Leyes de Kirchhoff? - Fórmulas y Ejemplos Prácticos.

Para resolver este circuito usando la Ley de Corrientes de Kirchhoff (LCK), procederemos paso a paso.

Paso 1: Identificar los nodos y las corrientes

En el diagrama, tenemos un nodo principal en la parte superior donde confluyen tres corrientes:

  • I_1​ es la corriente que fluye a través de R_1
  • I_2 es la corriente que fluye a través de R_3
  • I_3 es la corriente que fluye a través de R_2

Según la Ley de Corrientes de Kirchhoff (LCK) en el nodo:

I_1 = I_2 + I_3

Paso 2: Aplicar los valores conocidos

De los datos del circuito:

  • I_1 = 3 \, A
  • I_2 = 1 \, A
  • Necesitamos encontrar I_3

Sustituyendo los valores conocidos en la ecuación de la LCK:

3 = 1 + I_3

I_3 = 3 - 1 = 2 \, A

Por lo tanto, la corriente I_3 es de 2 \, A.

Paso 3: Verificación del resultado

Podemos verificar el resultado usando la Ley de Voltajes de Kirchhoff (LVK). Calcularemos la caída de voltaje a través de cada resistencia para asegurarnos de que la suma de los voltajes sea coherente con la fuente.

Cálculo de voltajes:
  1. La caída de voltaje en R_1:

V_{R_1} = I_1 \times R_1 = 3 \, A \times 10 \, \Omega = 30 \, V

  1. La caída de voltaje en R_2:

V_{R_2} = I_3 \times R_2 = 2 \, A \times 5 \, \Omega = 10 \, V

  1. La caída de voltaje en R_3​:

V_{R_3} = I_2 \times R_3 = 1 \, A \times 8 \, \Omega = 8 \, V

  1. La caída de voltaje en R_4:

V_{R_4} = I_2 \times R_4 = 1 \, A \times 4 \, \Omega = 4 \, V

La suma total de las caídas de voltaje debe ser igual a la fuente de voltaje. Sin embargo, el voltaje total del sistema está en los nodos que conectan a las resistencias.

El cálculo muestra que:

V_{fuente} = V_{R_1} - (V_{R_3} + V_{R_4}) + V_{R_2}​​

28=30−(8+4)+10

28= 30−12+10

28V=28V

Ley de Kirchhoff de Voltajes (LKV):

La Ley de Kirchhoff de Voltajes (LKV), también conocida como la Segunda Ley de Kirchhoff, establece que la suma algebraica de todas las diferencias de potencial (voltajes) en una malla es igual a cero. Esto significa que, en cualquier recorrido cerrado de un circuito, la energía total ganada por la corriente al pasar por fuentes de voltaje debe ser igual a la energía perdida al pasar por resistencias u otros componentes.

Conceptos Clave

  • Lazo cerrado: Un lazo cerrado es cualquier recorrido completo en un circuito que comienza y termina en el mismo punto, pasando por componentes sin repetir ramas.
  • Malla: Una malla es un tipo especial de lazo que no contiene otros lazos en su interior, siendo el camino más simple dentro de un circuito.
¿Qué son las Leyes de Kirchhoff? - Fórmulas y Ejemplos Prácticos.
  • Diferencia de potencial (voltaje): Es la energía por unidad de carga necesaria para mover la carga a través de un componente en el circuito. Se mide en voltios (V).
  • Caída de voltaje: Cuando la corriente pasa a través de una resistencia, pierde energía en forma de calor, lo que se traduce en una caída de voltaje.
  • Aumento de voltaje: Cuando la corriente pasa a través de una fuente de energía (como una batería), gana energía, lo que resulta en un aumento de voltaje.

Fórmula de la Ley de Kirchhoff de Voltajes

La expresión matemática de la LKV es la siguiente:

\sum V = 0

Esto significa que, al sumar todos los voltajes alrededor de un lazo cerrado, tanto los aumentos como las caídas de voltaje, el resultado total debe ser cero.

Ejemplo de Aplicación de la LKV

¿Qué son las Leyes de Kirchhoff? - Fórmulas y Ejemplos Prácticos.

Para resolver el circuito aplicando la Ley de Voltajes de Kirchhoff (LVK), procederemos paso a paso.

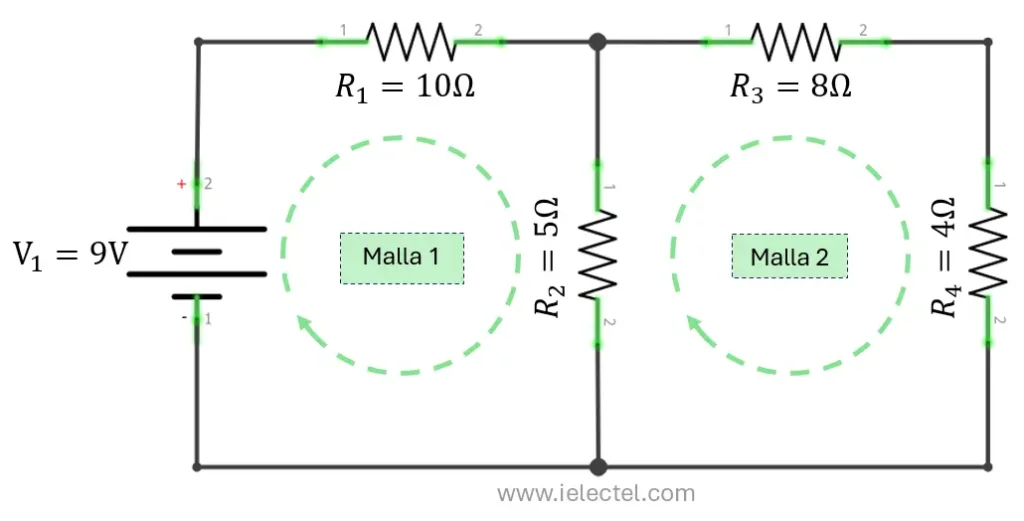
Paso 1: Identificación de las mallas y sus corrientes
¿Qué son las Leyes de Kirchhoff? - Fórmulas y Ejemplos Prácticos.

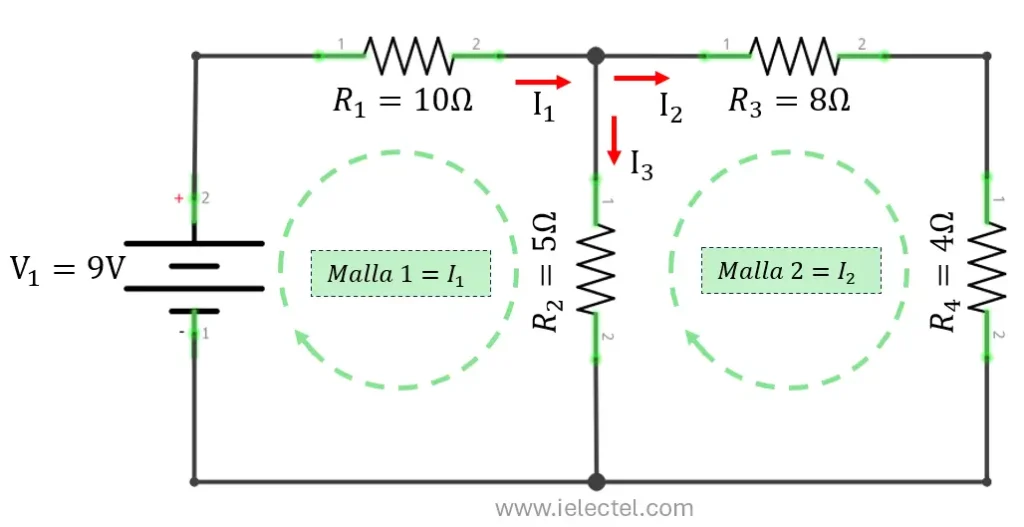
En el circuito tenemos dos mallas:

  • Malla 1 con corriente I_1
  • Malla 2 con corriente I_2

Hay una resistencia R_2​ que es compartida por ambas mallas, y por lo tanto, la corriente que pasa por ella es la diferencia entre I_1​ e I_2​. Para este caso, definimos la corriente a través de R_2​ como I_3 = I_1 - I_2.

Paso 2: Aplicar la Ley de Voltajes de Kirchhoff a cada malla
Malla 1

Para la malla 1, tenemos los siguientes elementos: V_1​, R_1, y R_2​. Aplicando la LVK y asumiendo una dirección horaria:

-V_1 + I_1 \cdot R_1 + I_3 \cdot R_2 = 0

Sustituyendo I_3 = I_1 - I_2​:

-9 + 10I_1 + 5(I_1 - I_2) = 0

-9 + 10I_1 + 5I_1 - 5I_2 = 0

15I_1 - 5I_2 = 9

Dividiendo toda la ecuación por 5:

3I_1 - I_2 = 1.8 \quad \text{(Ecuación 1)}

Nota: Dividir la ecuación por 5 es simplemente un proceso de simplificación matemática para obtener una forma más manejable de la ecuación. Al simplificar, se facilita el trabajo en los siguientes pasos y hace que los cálculos sean menos propensos a errores.

Malla 2

Para la malla 2, los elementos son R_3, R_4, y R_2​. Nuevamente aplicamos la LVK en sentido horario:

I_2 \cdot R_3 + I_2 \cdot R_4 + I_3 \cdot R_2 = 0

Sustituyendo I_3 = I_1 - I_2​:

8I_2 + 4I_2 + 5(I_1 - I_2) = 0

8I_2 + 4I_2 + 5I_1 - 5I_2 = 0

5I_1 + 7I_2 = 0 \quad \text{(Ecuación 2)}

Paso 3: Resolver el sistema de ecuaciones

Tenemos el siguiente sistema de ecuaciones:

  1. I_1 - I_2 = 1.8
  2. 5I_1 + 7I_2 = 0

Resolviendo estas ecuaciones simultáneamente:

Multiplicamos la Ecuación 1 por 7:

Multiplicamos la Ecuación 1 por 7 con el objetivo de eliminar una de las incógnitas cuando sumemos las dos ecuaciones, lo que es un paso crucial en la resolución de sistemas de ecuaciones lineales por el método de eliminación.

21I_1 - 7I_2 = 12.6

Ahora sumamos esta ecuación con la Ecuación 2:

21I_1 - 7I_2 + 5I_1 + 7I_2 = 12.6 + 0

26I_1 = 12.6

I_1 = \frac{12.6}{26} = 0.4846 \, \text{A}

Sustituyendo I_1 en la Ecuación 1:

3(0.4846) - I_2 = 1.8

1.4538 - I_2 = 1.8

I_2 = 1.4538 - 1.8

I_2 = -0.3462 \, \text{A}

La corriente I2I_2I2​ es negativa, lo que indica que la dirección de I2I_2I2​ es opuesta a la que habíamos asumido.

Paso 4: Calcular I_3

I_3 = I_1 - I_2 = 0.4846 - (-0.3462)

I_3 = 0.8308 \, \text{A}

Este es el procedimiento completo para resolver el circuito usando la Ley de Voltajes de Kirchhoff.

Paso 5: Verificación del resultado

Ahora, vamos a verificar los resultados obtenidos para asegurarnos de que sean correctos.

  • Reemplazar los valores de I_1​, I_2​ y I_3 en las ecuaciones originales

Recordemos las dos ecuaciones que obtuvimos aplicando la Ley de Voltajes de Kirchhoff:

  1. I_1 - I_2 = 1.8
  2. I_1 + 7I_2 = 0

Los valores obtenidos fueron:

  • I_1 = 0.4846 \, \text{A}
  • I_2 = -0.3462 \, \text{A}
  • I_3 = I_1 - I_2 = 0.8308 \, \text{A}
Verificación de la primera ecuación

3I_1 - I_2 = 1.8

Sustituyendo I_1 y I_2​:

3(0.4846) - (-0.3462) = 1.8

1.4538 + 0.3462 = 1.8

1.8 = 1.8 \quad \text{(Correcto)}

Verificación de la segunda ecuación

5I_1 + 7I_2 = 0

Sustituyendo I_1 y I_2​:

5(0.4846) + 7(-0.3462) = 0

2.423 - 2.423 = 0

0 = 0 \quad \text{(Correcto)}

Paso 6: Verificación con la Ley de Voltajes de Kirchhoff en cada malla
Para la Malla 1

La ecuación de la malla 1 era:

-V_1 + I_1 \cdot R_1 + I_3 \cdot R_2 = 0

Sustituyendo los valores:

-9 + 10(0.4846) + 5(0.8308) = 0

-9 + 4.846 + 4.154 = 0

0 = 0 \quad \text{(Correcto)}

Para la Malla 2

La ecuación de la malla 2 era:

I_2 \cdot R_3 + I_2 \cdot R_4 + I_3 \cdot R_2 = 0

Sustituyendo los valores:

8(-0.3462) + 4(-0.3462) + 5(0.8308) = 0

-2.7696 - 1.3848 + 4.154 = 0

0 = 0 \quad \text{(Correcto)}

Hemos verificado que las corrientes calculadas satisfacen tanto las ecuaciones originales obtenidas de la Ley de Voltajes de Kirchhoff como la relación de voltajes en ambas mallas. Por lo tanto, los valores de I_1​, I_2​, y I_3​ son correctos y el ejercicio está completamente verificado.

¿Por qué son importantes las Leyes de Kirchhoff?

Las leyes de Kirchhoff nos permiten analizar circuitos complejos en los que la Ley de Ohm por sí sola no es suficiente. Mientras que la Ley de Ohm (V = I \cdot R) es útil para circuitos simples, en los casos donde hay múltiples ramas o lazos, las leyes de Kirchhoff nos brindan un marco para resolver cada corriente y voltaje en el circuito.

Además, estas leyes son universales. Funcionan para circuitos en corriente continua (CC) y corriente alterna (CA), lo que las hace indispensables tanto en electrónica básica como en telecomunicaciones avanzadas.

Consejos para Principiantes

  • Define siempre direcciones: Antes de comenzar a escribir las ecuaciones, asegúrate de definir claramente la dirección de cada corriente. Esto te evitará confusiones cuando estés resolviendo el sistema de ecuaciones.
  • Consistencia con los signos: Al aplicar la LKV, ten cuidado con los signos. Si pasas por una resistencia en la dirección de la corriente, hay una caída de voltaje (resta); si vas en sentido contrario, hay un aumento (suma).
  • No te frustres: A veces, resolver los circuitos puede parecer complicado, pero con la práctica, los métodos se vuelven mucho más intuitivos.

Errores Comunes al Aplicar las Leyes de Kirchhoff

  1. Confusión en las direcciones de corriente: Un error frecuente es asignar incorrectamente las direcciones de las corrientes, lo que provoca resultados incorrectos en los cálculos. Si obtienes un valor negativo, no te preocupes: solo significa que la dirección de la corriente es opuesta a la que asumiste inicialmente.
  2. No respetar la convención de signos: Otro error común es olvidar sumar o restar correctamente los voltajes al recorrer un lazo, lo que genera resultados incorrectos.
  3. Ignorar la Ley de Ohm: Las leyes de Kirchhoff trabajan de la mano con la Ley de Ohm. Asegúrate de utilizarla correctamente cuando sustituyas valores de resistencia, corriente y voltaje en las ecuaciones.

Conclusión

Las Leyes de Kirchhoff son una herramienta esencial para cualquier persona que estudie electrónica o telecomunicaciones. Con ellas, puedes analizar circuitos de cualquier complejidad y encontrar fácilmente las corrientes y voltajes en cada parte del sistema. Ya sea que estés comenzando en el mundo de la electrónica o buscando refrescar tus conocimientos, estas leyes son el pilar de un buen análisis de circuitos. Sigue practicando, y con el tiempo, aplicar las leyes de Kirchhoff se convertirá en algo natural para ti.

Preguntas Frecuentes

¡Esperamos sinceramente que este post, repleto de contenido valioso, haya sido excepcionalmente útil en tu emocionante travesía hacia el fascinante mundo de la electrónica! 🌟 Te extendemos la invitación a explorar muchos más artículos, proyectos, contenido sobre equipos, software y más en nuestra página web.

Invita a otros a explorar: Comparte Ahora 📢

Entradas Relacionadas

Subscribe
Subscribe
Scroll al inicio